Question

12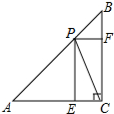．如图，已知△ABC是等腰直角三角形，∠ACB=90°，P为斜边AB上一点，PF⊥BC于点F，PE⊥AC于点E．若S_△APE=7，S_△PBF=2，则PC的长为（　　）

• A． 5
• B． 3$\sqrt{2}$
• C． $\sqrt{53}$
• D． 3$\sqrt{5}$

Answer 1

分析 由等腰直角三角形的性质得出∠A=∠B=45°，证出四边形PECF是矩形，得出PF=CE，证出△APE和△BPF是等腰直角三角形，得出AE=PE，BF=PF，再由三角形的面积得出PE²=14，CE²=PF²=4，由勾股定理求出PC的长即可．

解答 解：∵△ABC是等腰直角三角形，∠ACB=90°，
∴∠A=∠B=45°，
∵PF⊥BC于点F，PE⊥AC于点E，
∴∠PFB=∠PEA=90°，四边形PECF是矩形，
∴△APE和△BPF是等腰直角三角形，PF=CE，∠PEC=90°，
∴AE=PE，BF=PF，
∵S_△APE=$\frac{1}{2}$AE•PE=$\frac{1}{2}$PE²=7，S_△PBF=$\frac{1}{2}$PF•BF=$\frac{1}{2}$PF²=2，
∴PE²=14，CE²=PF²=4，
∴PC=$\sqrt{P{E}^{2}+C{E}^{2}}$=$\sqrt{14+4}$=3$\sqrt{2}$；
故选：B．

点评 本题考查了等腰直角三角形的判定与性质、矩形的判定与性质、勾股定理；熟练掌握等腰直角三角形的判定与性质，运用勾股定理求出PC是解决问题的关键．