题目内容
某中学对九年级准备选考1分钟跳绳的同学进行测试,测试结果如下表:频数分布表
| 组别 | 跳绳(次/1分钟) | 频数 |
| 第1组 | 190~199 | 5 |
| 第2组 | 180~189 | 11 |
| 第3组 | 170~179 | 23 |
| 第4组 | 160~169 | 33 |
| 第5组 | 150~159 | 8 |
(1)此次测试成绩的中位数落在第______组中;
(2)如果成绩达到或超过180次/分钟的同学可获满分,那么本次测试中获得满分的人数占参加测试人数的______%;
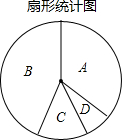
(3)如果该校九年级参加体育测试的总人数为200人,若要绘制一张统计该校各项目选考人数分布的扇形图(如图),图中A所在的扇形表示参加选考1分钟跳绳的人数占测试总人数的百分比,那么该扇形的圆心角应为______°;
(4)如果此次测试的平均成绩为171次/分钟,那么这个成绩是否可用来估计该校九年级学生跳绳的平均水平?为什么?

【答案】分析:(1)将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.(2)获得满分的人数÷参加测试的总人数;
(3)360°×百分比=扇形圆心角;
(4)利用样本估计数据总体情况的定义分析.
解答:解:(1)数据个数:5+11+23+33+8=80,位置处于中间数是第40和41个,落在第4小组,
(2)(5+11)÷80=20%,
(3)360°×40%=144°;
(4)不可以,选考跳绳的同学说明对跳绳比较擅长,这样一来,样本不具有随机性.所以不能代表整体的水平.
点评:此题主要考查了中位数,圆心角的计算,样本估计总体的知识,题目比较基础.
(3)360°×百分比=扇形圆心角;
(4)利用样本估计数据总体情况的定义分析.
解答:解:(1)数据个数:5+11+23+33+8=80,位置处于中间数是第40和41个,落在第4小组,
(2)(5+11)÷80=20%,
(3)360°×40%=144°;
(4)不可以,选考跳绳的同学说明对跳绳比较擅长,这样一来,样本不具有随机性.所以不能代表整体的水平.
点评:此题主要考查了中位数,圆心角的计算,样本估计总体的知识,题目比较基础.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 某中学对九年级准备选考1分钟跳绳的同学进行测试,测试结果如下表:
某中学对九年级准备选考1分钟跳绳的同学进行测试,测试结果如下表:频数分布表:
| 组别 | 跳绳(次/1分钟) | 频数 |
| 第1组 | 190~199 | 5 |
| 第2组 | 180~189 | 11 |
| 第3组 | 170~179 | 23 |
| 第4组 | 160~169 | 33 |
(1)此次测试成绩的中位数落在第
(2)如果成绩达到或超过180次/分钟的同学可获满分,那么本次测试中获得满分的人数占参加测试人数的
(3)如果该校九年级参加体育测试的总人数为200人,若要绘制一张统计该校各项目选考人数分布的扇形图(如图),图中A所在的扇形表示参加选考1分钟跳绳的人数占测试总人数的百分比,那么该扇形的圆心角应为
(4)如果此次测试的平均成绩为171次/分钟,那么这个成绩是否可用来估计该校九年级学生跳绳的平均水平?为什么?
某中学对九年级准备选考1分钟跳绳的同学进行测试,测试结果如下表:
频数分布表
| 组别 | 跳绳(次/1分钟) |
|
| 第1组 | 190~199 | 5 |
| 第2组 | 180~189 | 11 |
| 第3组 | 170~179 | 23 |
| 第4组 | 160~169 | 33 |
| 第5组 | 150~159 | 8 |
|
(1)此次测试成绩的中位数落在第 ▲ 组中;
(2)如果成绩达到或超过180次/分钟的同学可获满分,那么本次测试中获得满分的人数占参加测试人数的 ▲ %;
(3)如果该校九年级参加体育测试的总人数为200人,若要绘制一张统计该校各项目选考人数分布的扇形图(如22题图),图中A所在的扇形表示参加选考1分钟跳绳的人数占测试总人数的百分比,那么该扇形的圆心角应为 ▲ °;
(4)如果此次测试的平均成绩为171次/分钟,那么这个成绩是否可用来估计该校九年级学生跳绳的平均水平?为什么?
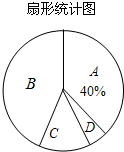 20、某中学对九年级准备选考1分钟跳绳的同学进行测试,测试结果如下表:
20、某中学对九年级准备选考1分钟跳绳的同学进行测试,测试结果如下表:
 频数
频数