题目内容
3. 已知:如图,在△ABC中,点M、M分别在边AC、BC上,点P是AN上一点,且∠ABM=∠APM=∠C.
已知:如图,在△ABC中,点M、M分别在边AC、BC上,点P是AN上一点,且∠ABM=∠APM=∠C.(1)求证:AM•AC=AP•AN;
(2)求证:∠ABP=∠ANB.
分析 (1)由∠PAM=∠CAN,∠APM=∠C,可证得△APM∽△ACN,然后由相似三角形的对应边成比例,证得结论;
(2)由∠ABM=∠C,∠BAM=∠CAB,可证得△ABM∽△ACB,即可得AB2=AM•AC,又由AM•AC=AP•AN,可得AB:AP=AN:AB,则可证得△BAP∽△NAB,继而证得结论.
解答 证明:(1)∵∠PAM=∠CAN,∠APM=∠C,
∴△APM∽△ACN,
∴AP:AC=AM:AN,
∴AM•AC=AP•AN;
(2)∵∠ABM=∠C,∠BAM=∠CAB,
∴△ABM∽△ACB,
∴AB:AC=AM:AB,
∴AB2=AM•AC,
∵AM•AC=AP•AN,
∴AB2=AP•AN,
∴AB:AP=AN:AB,
∵∠BAP=∠NAB,
∴△BAP∽△NAB,
∴∠ABP=∠ANB.
点评 此题考查了相似三角形的判定与性质.注意掌握相似三角形的对应边成比例与有两角对应相等的三角形相似定理的应用是解此题的关键.

练习册系列答案
相关题目
14. 如图,△ABC内有一点P,过P点分别作MF∥BC,GD∥AB,EN∥AC,且BD:DE:EC=1:2:3,则S△PMN:S△PDE:S△PGF为( )
如图,△ABC内有一点P,过P点分别作MF∥BC,GD∥AB,EN∥AC,且BD:DE:EC=1:2:3,则S△PMN:S△PDE:S△PGF为( )
 如图,△ABC内有一点P,过P点分别作MF∥BC,GD∥AB,EN∥AC,且BD:DE:EC=1:2:3,则S△PMN:S△PDE:S△PGF为( )
如图,△ABC内有一点P,过P点分别作MF∥BC,GD∥AB,EN∥AC,且BD:DE:EC=1:2:3,则S△PMN:S△PDE:S△PGF为( )| A. | 1:2:3 | B. | 1:2:4 | C. | 1:4:6 | D. | 1:4:9 |
14.$\sqrt{18}$-$\sqrt{2}$的值是( )
| A. | 4 | B. | $\sqrt{16}$ | C. | 2$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
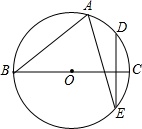 已知:如图,⊙O的直径BC=2,点A在⊙O上,∠ABC=30°,D是$\widehat{AC}$的中点,弦DE⊥BC,连接AE
已知:如图,⊙O的直径BC=2,点A在⊙O上,∠ABC=30°,D是$\widehat{AC}$的中点,弦DE⊥BC,连接AE