题目内容
已知,如图,线段AB上有任一点M,分别以AM,BM为边长作正方形AMFE、MBCD.正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点,则直线MN的情况是( )

| A.定直线 | B.经过定点 |
| C.一定不过定点 | D.以上都有可能 |


连接NA,NB.如图,
∵四边形AMFE、MBCD都是正方形,
∴在⊙O中,∠ANM=45°;在⊙O′中,∠BNM=45°,
即∠ANM=90°,所以点N总在以AB为直径的圆上,
延长NM交以AB为直径的圆于P点.
∵∠ANM=∠BNM=45°,
∴弧PA=弧PB,即P为半圆的中点.由于AB固定,则点P为定点.
所以直线MN过定点P.
故选B.

练习册系列答案
相关题目
 已知,如图,线段AB⊥BC,DC⊥BC,垂足分别为点B、C.
已知,如图,线段AB⊥BC,DC⊥BC,垂足分别为点B、C. 2、已知,如图,线段AB上有任一点M,分别以AM,BM为边长作正方形AMFE、MBCD.正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点,则直线MN的情况是( )
2、已知,如图,线段AB上有任一点M,分别以AM,BM为边长作正方形AMFE、MBCD.正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点,则直线MN的情况是( ) 已知:如图,线段AB=10cm,点O是线段AB的中点,线段BC=3cm,则线段OC=
已知:如图,线段AB=10cm,点O是线段AB的中点,线段BC=3cm,则线段OC=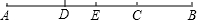
 已知:如图,线段AB、DE表示一个斜靠在墙上的梯子的两个不同的位置,若CB=3m,∠ABC=45°,要使∠EDC=60°,则需BD=
已知:如图,线段AB、DE表示一个斜靠在墙上的梯子的两个不同的位置,若CB=3m,∠ABC=45°,要使∠EDC=60°,则需BD=