题目内容
如图，直线y=k1x+b与双曲线y=
相交于A（1，2）、B（m，﹣1）两点．
（1）求直线和双曲线的解析式；
（2）若A1（x1，y1），A2（x2，y2），A3（x3，y3）为双曲线上的三点，且x1＜x2＜0＜x3，请直接写出y1，y2，y3的大小关系式；
（3）观察图象，请直接写出不等式k1x+b＞
的解集．
相交于A（1，2）、B（m，﹣1）两点．（1）求直线和双曲线的解析式；
（2）若A1（x1，y1），A2（x2，y2），A3（x3，y3）为双曲线上的三点，且x1＜x2＜0＜x3，请直接写出y1，y2，y3的大小关系式；
（3）观察图象，请直接写出不等式k1x+b＞
的解集．解：（1）∵双曲线y=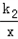
经过点A（1，2），
∴k2=2，
∴双曲线的解析式为：y=
．
∵点B（m，﹣1）在双曲线y=
上，
∴m=﹣2，则B（﹣2，﹣1）．
由点A（1，2），B（﹣2，1）在直线y=k1x+b上，
得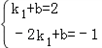
，
解得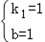
，
∴直线的解析式为：y=x+1．
（2）∵在第三象限内y随x的增大而减小，故y2＜y1＜0，
又∵y3是正数，故y3＞0，
∴y2＜y1＜y3．
（3）由图可知，x＞1或﹣2＜x＜0．
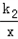经过点A（1，2），∴k2=2，
∴双曲线的解析式为：y=
．∵点B（m，﹣1）在双曲线y=
上，∴m=﹣2，则B（﹣2，﹣1）．
由点A（1，2），B（﹣2，1）在直线y=k1x+b上，
得
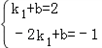，解得
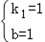，∴直线的解析式为：y=x+1．
（2）∵在第三象限内y随x的增大而减小，故y2＜y1＜0，
又∵y3是正数，故y3＞0，
∴y2＜y1＜y3．
（3）由图可知，x＞1或﹣2＜x＜0．
练习册系列答案
阅读快车系列答案
相关题目
11、如图，直线y1=k1x+a与y2=k2x+b的交点坐标为（1，2），则使y1＜y2的x的取值范围为
9、如图，直线y1=k1x+a与y2=k3x+b的交点坐标为（1，2），则使y1＜y2的x的取值范围为（ ）
如图，直线y=k1x与双曲线y=
（2013•阜宁县一模）如图，直线y=k1x-b与双曲线
（2013•甘井子区一模）如图，直线y=k1x+b与双曲线