题目内容
15.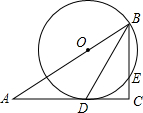 如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
分析 (1)连接OD,由BD为角平分线得到一对角相等,根据OB=OD,等边对等角得到一对角相等,等量代换得到一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODA为直径,即可得证;
(2)过O作OG垂直于BE,可得出四边形ODCG为矩形,在直角三角形OBG中,利用勾股定理求出BG的长,由垂径定理可得BE=2BG.
解答 (1)证明:连接OD,
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,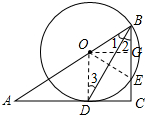
∴∠ODA=90°,
则AC为圆O的切线;
(2)解:过O作OG⊥BC,连接OE,
∴四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BE,OB=OE,
∴BE=2BG=12.
解得:BE=12.
点评 此题考查了切线的判定,相似三角形的判定与性质,平行线的判定与性质,以及等腰三角形的性质,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
3.已知正比例函数y=3x的图象经过点(1,m),则m的值为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -3 |
20.不等式组$\left\{\begin{array}{l}{2x+2>x}\\{3x<x+2}\end{array}\right.$的解集是( )
| A. | x>-2 | B. | x<1 | C. | -1<x<2 | D. | -2<x<1 |
12.为了解我市八年级10000名学生的身高,从中抽取了500名学生,对其身高进行统计分析,以下说法正确的是( )
| A. | 10000名学生是总体 | B. | 本次调查采用的是普查 | ||
| C. | 样本容量是500名学生 | D. | 每个学生的身高是个体 |
 如图,平行四边形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件AC⊥BD或∠AOB=90°或AB=BC使其成为菱形(只填一个即可).
如图,平行四边形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件AC⊥BD或∠AOB=90°或AB=BC使其成为菱形(只填一个即可).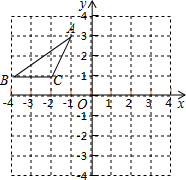 如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)(-2,1),先将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)(-2,1),先将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2. 如图,平行线AB,CD被直线AE所截,∠1=50°,则∠A=50°.
如图,平行线AB,CD被直线AE所截,∠1=50°,则∠A=50°.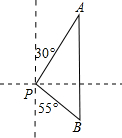 如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为11海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).
如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为11海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).