题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,且
上一点,且![]() ,点
,点![]() 在边
在边![]() 上,过点
上,过点![]() 、
、![]() 、
、![]() 作圆
作圆![]() ,交边
,交边![]() 或其延长线于
或其延长线于![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,设
,设![]() (
(![]() ).
).
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求弧
,求弧![]() 的长;
的长;
(4)若圆![]() 经过矩形的两个顶点时,直接写出
经过矩形的两个顶点时,直接写出![]() 的值.
的值.
(注:![]() ,
,![]() ,
,![]() )
)
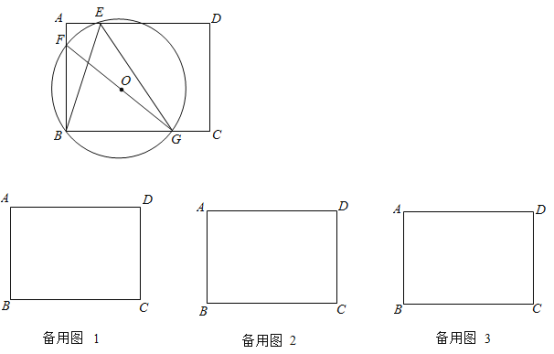
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)3或
;(4)3或![]()
【解析】
(1)由题意得∠FGE=∠ABE,根据锐角三角函数的定义可得出结论;
(2)连接EF,OE,证明Rt△BFG≌Rt△EFG(HL),得出BF=EF,由勾股定理得出x2=(6-x)2+32,解得![]() .
.
(3)证明△ABE∽△EGF,得出![]() ,求出GF,EG,由锐角三角函数可求出∠FGE,由弧长公式可得出答案;
,求出GF,EG,由锐角三角函数可求出∠FGE,由弧长公式可得出答案;
(4)分两种情况:①若圆O经过矩形的顶点C时,②若圆O经过矩形的顶点D时,过点G作GM⊥AD,垂足M落在AD的延长线,由勾股定理可求出答案.
(1)![]()
∴![]() ,
,
∵![]() ,
,
∴![]()
(2)连接EF,OE,
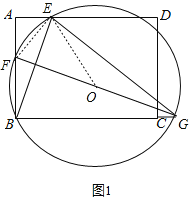
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() 是圆
是圆![]() 的直径,
的直径,
∴![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
在Rt△AEF中,∵EF2=AE2+AF2,
∴x2=(6-x)2+32,
解得![]()
(3)∵BF=2,
∴AF=AB-BF=6-2=4,
∵AE=3,
∴![]() ,
,
∵![]() ,
,
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
∴弧![]() 的长
的长![]()
(4)3或![]()
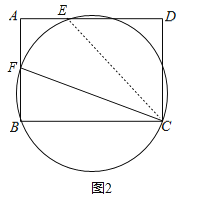
①若圆![]() 经过矩形的顶点
经过矩形的顶点![]() 时,
时,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() ,∴
,∴![]()
②若圆![]() 经过矩形的顶点
经过矩形的顶点![]() 时,过
时,过![]() 作
作![]() ,垂足
,垂足![]() 落在
落在![]() 的延长线上,
的延长线上,
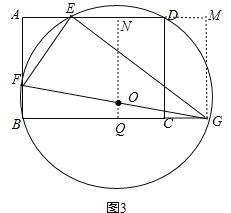
易得四边形![]() 是矩形,四边形
是矩形,四边形![]() 是矩形,过
是矩形,过![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.

【题目】2020年春节,一场突如其来的新型冠状肺炎病毒疫情在武汉突发,为响应党中央号召,在“支援武汉,防控疫情”的过程中,某省计划组织1441名医护人员的“援汉”团队前往武汉进行支援,经过研究,决定租用当地租车公司一共62辆![]() 、
、![]() 两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 380元 |
| 20人 | 280元 |
注:载客量指的是每辆客车最多可载医护人员的人数.
(1)设租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过19900元,一共有几种租车方案?哪种租车方案最省钱?