题目内容
【题目】对于某一函数给出如下定义:若存在实数![]() ,当其自变量的值为
,当其自变量的值为![]() 时,其函数值等于
时,其函数值等于![]() ,则称
,则称![]() 为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差
为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差![]() 称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度
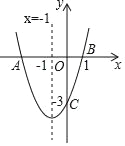
称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度![]() 为零.例如,图1中的函数有0,1两个不变值,其不变长度
为零.例如,图1中的函数有0,1两个不变值,其不变长度![]() 等于1.
等于1.
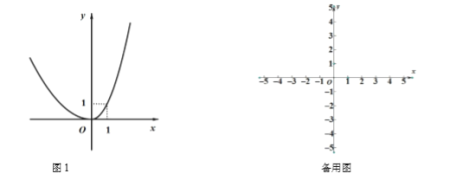
(1)分别判断函数![]() ,
,![]() 有没有不变值?如果有,请写出其不变长度;
有没有不变值?如果有,请写出其不变长度;
(2)函数![]() 且
且![]() ,求其不变长度
,求其不变长度![]() 的取值范围;
的取值范围;
(3)记函数![]() 的图像为
的图像为![]() ,将
,将![]() 沿
沿![]() 翻折后得到的函数图像记为
翻折后得到的函数图像记为![]() ,函数
,函数![]() 的图像由
的图像由![]() 和
和![]() 两部分组成,若其不变长度
两部分组成,若其不变长度![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】
(1)不存在不变值;存在不变值,q=3;(2)0≤q≤2![]() ;(3)
;(3)![]() ≤m≤4 或m<-0.5.
≤m≤4 或m<-0.5.
【解析】
(1)由题意得:y=x-3=x,无解,故不存在不变值;y=x2-2=x,解得:x=2或-1,即可求解;
(2)由题意得:y=x2-bx+1=x,解得:x= ![]() ,即可求解;
,即可求解;
(3)由题意得:函数G的不变点为:2m-1+ ![]() 、2m-1-
、2m-1- ![]() 、0、4;分x=m为G1的左侧、x=m为G1的右侧,两种情况分别求解即可.
、0、4;分x=m为G1的左侧、x=m为G1的右侧,两种情况分别求解即可.
解:(1)由题意得:y=x-3=x,无解,故不存在不变值;
y=x2-2=x,解得:x=2或-1,故存在不变值,q=2-(-1)=3;
(2)由题意得:y=x2-bx+1=x,
解得:x=![]() ,
,
q=![]() ,1≤b≤3,
,1≤b≤3,
解得:0≤q≤2![]() ;
;
(3)由题意得:y=x2-3x沿x=m对翻折后,
新抛物线的顶点为(2m-![]() ,-
,-![]() ),
),
则新函数G2的表达式为:y=x2-(4m-3)x+(4m2-6m),
当y=x时,整理得:x2-(4m-2)x+(4m2-6m)=0,
x=2m-1±![]() ,
,
即G2的不变点是2m-1+![]() 和2m-1-
和2m-1-![]() ;
;
G1的不变点是:0和4;
故函数G的不变点为:2m-1+![]() 、2m-1-
、2m-1-![]() 、0、4,
、0、4,
这4个不变点最大值的可能是2m-1+![]() 、4,最小值可能2m-1-
、4,最小值可能2m-1-![]() 、0,
、0,
----当x=m为G1对称轴x=的左侧时,
①当最大值为2m-1+![]() 时,
时,
当最小值为2m-1-![]() 时,
时,
即:0≤2m-1+![]() -(2m-1-
-(2m-1-![]() )≤4,
)≤4,
解得:0≤m≤![]() ;
;
当最小值为0时,
同理可得:0≤m≤![]() ;
;
②当最大值为4时,
最小值为2m-1-![]() 即可(最小值为0,符合条件),
即可(最小值为0,符合条件),
即0≤4-(2m-1-![]() )≤4,
)≤4,
解得:m=![]() ;
;
综上:0≤m≤![]() ;
;
----当x=m为G1对称轴x=![]() 的右侧时,
的右侧时,
同理可得:![]() ≤m≤
≤m≤![]() ;
;
故:![]() ≤m≤4 或m<-0.5.
≤m≤4 或m<-0.5.

【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.