题目内容
19.已知⊙O的弦AB长为2,C是⊙O上一点,若∠ACB=45°,则△ABC的面积的最大值为$\sqrt{2}$+1.分析 首先过C作CM⊥AB于M,由弦AB已确定,可得要使△ABC的面积最大,只要CM取最大值即可,即可得当CM过圆心O时,CM最大,然后由圆周角定理,证得△AOB是等腰直角三角形,则可求得CM的长,继而求得答案.
解答 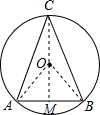 解:过C作CM⊥AB于M,
解:过C作CM⊥AB于M,
∵弦AB已确定,
∴要使△ABC的面积最大,只要CM取最大值即可,
如图所示,当CM过圆心O时,CM最大,
∵CM⊥AB,CM过O,
∴AM=BM(垂径定理),
∴AC=BC,
∵∠AOB=2∠ACB=2×45°=90°,
∴OM=AM=$\frac{1}{2}$AB=$\frac{1}{2}$×2=1,
∴OA=$\sqrt{O{M}^{2}+A{M}^{2}}$=$\sqrt{2}$,
∴CM=OC+OM=$\sqrt{2}$+1,
∴S△ABC=$\frac{1}{2}$AB•CM=$\frac{1}{2}$×2×($\sqrt{2}$+1)=$\sqrt{2}$+1.
故答案为:$\sqrt{2}$+1.
点评 此题考查了圆周角定理以及等腰直角三角形性质.注意得到当CM过圆心O时,CM最大是关键.

练习册系列答案
相关题目
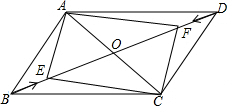 如图,在?ABCD中,对角线BD=8cm.AC=4cm.点E从点B出发沿BD方向以1cm/s的速度向点D运动,同时点F从点D出发沿着DB方向以同样的速度向点B运动,设点E,F运动的时间为t(s),其中0<t<8.
如图,在?ABCD中,对角线BD=8cm.AC=4cm.点E从点B出发沿BD方向以1cm/s的速度向点D运动,同时点F从点D出发沿着DB方向以同样的速度向点B运动,设点E,F运动的时间为t(s),其中0<t<8.