题目内容
某医药研究所开发一种新药.在试验药效时发现,如果成人按规定剂量服用,那么服药2h后血液中含药量最高,达到每毫升6μg(1μg=10-3mg),接着逐步衰减,10h后血液中含药量为每毫升3μg.若每毫升血液中含药量y(μg)随时间x(h)的变化如图所示,则当成人按规定剂量服药后:
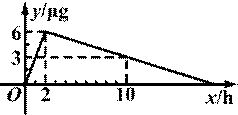
(1)当0≤x≤2时,y=3x.
②当x>2时, 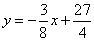 .
.
(2)有效时间是6h.
【解析】(1)根据图象写出函数解析式,前面2h对应的线段是正比例函数的图象,设为y=k1x(k1≠0),把(2,6)代入即可求出k1.当x>2时,图象对应的是一次函数,设为y=k2x+b(k2≠0).把(2,6),(10,3)代入即可求出k2,b.(2)由图象可知,有两个时刻成人血液中的含药量为4μg,这两个时刻间的时间段内含药量高于4μg.
解:(1)根据图象可知,当0≤x≤2时,y是x的正比例函数;当x>2时,y是x的一次函数.
①当0≤x≤2时,设y=k1x(k1≠0),把(2,6)代入y=k1x,得k1=3.
所以当0≤x≤2时,y=3x.
②当x>2时,设y=k2x+b(k2≠0),把(2,6),(10,3)代入y=k2x+b中,得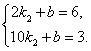 解得
解得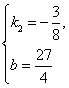
所以当x>2时,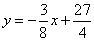 .
.
(2)把y=4代入y=3x,得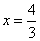 ;把y=4代入
;把y=4代入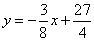 ,得
,得 .因为
.因为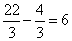 ,所以这个有效时间是6h.
,所以这个有效时间是6h.
【难度】一般

练习册系列答案
相关题目
 ,
, ,那么向量
,那么向量 用向量
用向量 、
、 表示为 .
表示为 .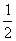 ,
,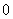 ),(-
),(-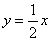 的图象相交于点(2,a).
的图象相交于点(2,a).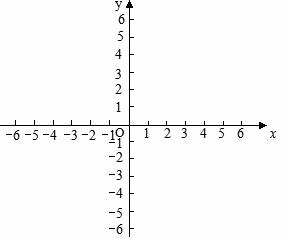
 ABCD,如图1和图2.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶.供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.
ABCD,如图1和图2.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶.供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.




 -
- ;
; 的解是 .
的解是 .