题目内容
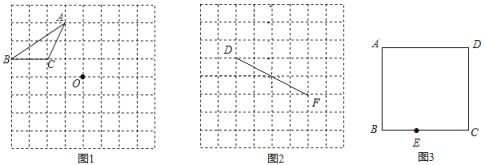
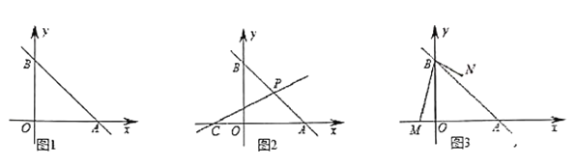
【题目】如图1,已知直线![]() :
:![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() .
.
(1)直接写出![]() 的值为______.
的值为______.
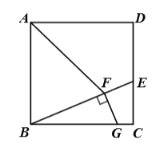
(2)如图2,![]() 为
为![]() 轴负半轴上一点,过
轴负半轴上一点,过![]() 点的直线
点的直线![]() :
:![]() 经过
经过![]() 的中点
的中点![]() ,点
,点![]() 为
为![]() 轴上一动点,过
轴上一动点,过![]() 作
作![]() 轴分别交直线
轴分别交直线![]() 、
、![]() 于
于![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
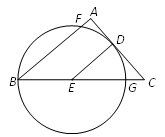
(3)如图3,已知点![]() ,点
,点![]() 为直线
为直线![]() 右侧一点,且满足
右侧一点,且满足![]() ,求点
,求点![]() 坐标.
坐标.
【答案】(1)k=-1;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)将![]() 代入
代入![]() ,求解即可得出;
,求解即可得出;
(2)先求得直线![]() 为
为![]() ,用含t的式子表示MN,根据
,用含t的式子表示MN,根据![]() 列出方程
列出方程![]() ,分三种情况讨论,可得到
,分三种情况讨论,可得到![]() 或
或![]() ;
;
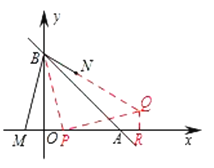
(3)在![]() 轴上取一点
轴上取一点![]() ,连接
,连接![]() ,作
,作![]() 交直线
交直线![]() 于
于![]() ,作
,作![]() 轴于
轴于![]() ,再证出
,再证出![]() ,得到直线
,得到直线![]() 的解析式为
的解析式为![]() ,将
,将![]() 代入
代入![]() ,得
,得![]() ,可得出
,可得出![]() .
.
解:(1)将![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() .
.
故答案为:![]()
(2)∵在直线![]() 中,令
中,令![]() ,得
,得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,代入
,代入![]() ,得
,得![]() ,
,
∴直线![]() 为
为![]() ,
,
∵![]() 轴分别交直线
轴分别交直线![]() 、
、![]() 于
于![]() 、
、![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,分情况讨论:
,分情况讨论:
①当![]() 时,
时,![]() ,解得:
,解得:![]() .
.
②当![]() 时,
时,![]() ,解得:
,解得:![]() .
.
③当![]() 时,
时,![]() ,解得:
,解得:![]() ,舍去.
,舍去.
综上所述:![]() 或
或![]() .
.
(3)在![]() 轴上取一点
轴上取一点![]() ,连接
,连接![]() ,作
,作![]() 交直线
交直线![]() 于
于![]() ,作
,作![]() 轴于
轴于![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】在“元旦”期间,平价商场对该商场商品进行如下的优惠促销活动:
打折前一次性购物总金额 | 优惠措施 |
小于等于 400 元 | 不优惠 |
超过 400 元,但不超过 600元 | 按售价打九折 |
超过 600 元 | 其中 600 元部分八折优惠,超过 600 元的部分打六折优惠 |
按上述优惠条件,若小华一次性购买售价为 80 元/件的商品 n 件时,实际付款 504 元, 则 n=_____.