题目内容
5.在Rt△ABC中,∠C=90°,AC=3,BC=4,那么cosB的值是$\frac{4}{5}$.分析 在直角△ABC中利用勾股定理求得AB的长,然后利用三角函数的定义求解.
解答  解:在直角△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
解:在直角△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
则cosB=$\frac{BC}{AB}$=$\frac{4}{5}$.
故答案是:$\frac{4}{5}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.某股票上周五的收盘价为39.60元,本周此股票每日的涨跌情况如下表:
(当天的收盘价高出前一个交易日的收盘价2.1元记作+2.1元;当天的收盘价低于前一个交易日的收盘价1.5元记作-1.5元.)
(1)本周星期四此股票的收盘价是多少?
(2)若本周星期五此股票的收盘价为42.6元,求a的值,并说明星期五此股票是涨了还是跌了,涨或跌了多少元?
| 某股票一周涨跌情况表(单位:元) | ||||
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| +2.1 | -1.8 | +3.8 | -0.6 | A |
(1)本周星期四此股票的收盘价是多少?
(2)若本周星期五此股票的收盘价为42.6元,求a的值,并说明星期五此股票是涨了还是跌了,涨或跌了多少元?
17.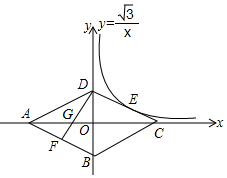 已知如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
已知如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
 已知如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
已知如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\sqrt{3}$+2 | C. | 2$\sqrt{3}$+1 | D. | $\frac{3\sqrt{3}}{2}$+1 |
14.下列四个汉字中,属于轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

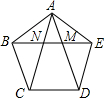 如图,在正五边形ABCDE中,对角线AD、AC与EB分别交于点M、N.
如图,在正五边形ABCDE中,对角线AD、AC与EB分别交于点M、N.


