题目内容
(1)如图,EF是⊙O的直径,请仅用尺规作出该圆的内接正方形ABCD,要求所作正方形的一组对边AD、BC垂直于EF.(见示意图;不写作法,但须保留作图痕迹);(2)连接EA、EB,求出∠EAD、∠EBC的度数.

【答案】分析:(1)作出八等分点,即可得到圆内接正方形;
(2)求出相应圆心角的度数,根据圆周角等于圆心角的一半,即可解答.
解答: 解:(1)作①EF的中垂线(1分),
解:(1)作①EF的中垂线(1分),
②直角的平分线OD(1分),
③8等分弧,完成正方形(2分).
(作图(4分),其他方法只要痕迹清楚、正确,同样给分)
(2)连接OD,OC,
因为 =
= 圆周,所以∠EOD=360°×
圆周,所以∠EOD=360°× =45°,
=45°,
所以∠EAD=45°× =22.5°.
=22.5°.
因为 =3
=3 ,
,
所以∠EBC=3∠EAD=3×22.5°=67.5°.
点评:此题结合多边形和圆的关系,考查了基本作图、圆周角与圆心角的关系,是一道基础题.
(2)求出相应圆心角的度数,根据圆周角等于圆心角的一半,即可解答.
解答:
 解:(1)作①EF的中垂线(1分),
解:(1)作①EF的中垂线(1分),②直角的平分线OD(1分),
③8等分弧,完成正方形(2分).
(作图(4分),其他方法只要痕迹清楚、正确,同样给分)
(2)连接OD,OC,
因为
 =
= 圆周,所以∠EOD=360°×
圆周,所以∠EOD=360°× =45°,
=45°,所以∠EAD=45°×
 =22.5°.
=22.5°.因为
 =3
=3 ,
,所以∠EBC=3∠EAD=3×22.5°=67.5°.
点评:此题结合多边形和圆的关系,考查了基本作图、圆周角与圆心角的关系,是一道基础题.

练习册系列答案
相关题目
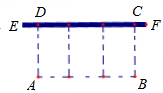 23、如图,EF是一面长18米的墙,用总长为32米的木栅栏(图中的虚线)围一个矩形场地,中间还要隔成三块.设与墙头垂直的边AD长为x米,
23、如图,EF是一面长18米的墙,用总长为32米的木栅栏(图中的虚线)围一个矩形场地,中间还要隔成三块.设与墙头垂直的边AD长为x米,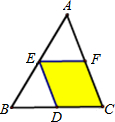 16、如图,EF是△ABC的中位线,将△AEF沿AB方向平移到△EBD的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面积为
16、如图,EF是△ABC的中位线,将△AEF沿AB方向平移到△EBD的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面积为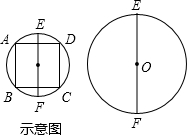 (1)如图,EF是⊙O的直径,请仅用尺规作出该圆的内接正方形ABCD,要求所作正方形的一组对边AD、BC垂直于EF.(见示意图;不写作法,但须保留作图痕迹);
(1)如图,EF是⊙O的直径,请仅用尺规作出该圆的内接正方形ABCD,要求所作正方形的一组对边AD、BC垂直于EF.(见示意图;不写作法,但须保留作图痕迹);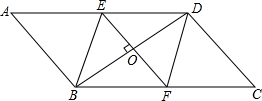 别交于点E、F.
别交于点E、F.  如图,EF是⊙O的直径.
如图,EF是⊙O的直径.