Question

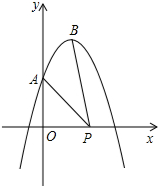如图，抛物线y=-

4

9

x²+

8

3

x+2与y轴交于点A，顶点为B，点P是x轴上的一个动点，求线段PA与PB中较长的线段减去较短的线段的差的最小值与最大值，并求出相应的点P的坐标．

Answer 1

考点：轴对称-最短路线问题,二次函数的性质

专题：

分析：根据抛物线的解析式求得A的坐标，顶点B的坐标，设P（x，0），根据当PA=PB是线段PA与PB的差的最小，即可求得最小值和P的坐标；根据当P、A、B在一条直线上时，线段PA与PB的差最大，根据PB=PA+AB即可求得最大值和最大值时P的坐标．

解答：解：∵抛物线y=-

4

9

x²+

8

3

x+2与y轴交于点A，
∴A（0，2），
∵y=-

4

9

x²+

8

3

x+2=-

4

9

（x-3）²+6，
∴顶点B（3，6），
设P（x，0），
当PA=PB是线段PA与PB的差的最小，PA-PB=0，
∵A（0，2），B（3，6），
∴PA²=x²+2²=x²+4，PB²=（x-3）²+6²，
∴x²+4=（x-3）²+6²，解得：x=

41

6

，
∴P（

41

6

，0），
当P、A、B在一条直线上时，线段PA与PB的差的最大；
∵A（0，2），B（3，6），
∴PA=

x2+22

，PB=

(x-3)2+62

，AB=

32+(6-2)2

=5，
∴PB=PA+AB，即

(x-3)2+62

=5+

x2+22

，
解得x=-

3

2

，
∴P（-

3

2

，0）．PA=

5

2

，PB=

15

2

，
∴PB-PA=5，
所以线段PA与PB中较长的线段减去较短的线段的差的最小值是0，此时点P的坐标为（

41

6

，0）；线段PA与PB中较长的线段减去较短的线段的差的最大值为5，此时点P的坐标为（-

3

2

，0）．

点评：本题考查了轴对称-最短路线问题，二次函数的性质，勾股定理的应用等，当P、A、B在一条直线上时，线段PA与PB的差的最大是关键．