题目内容
 如图,PB切⊙O于点B,OP交⊙O于点A,BC⊥PO于点C,若OA=6,OP=8,则AC=
如图,PB切⊙O于点B,OP交⊙O于点A,BC⊥PO于点C,若OA=6,OP=8,则AC=考点:切线的性质
专题:
分析:连接OB,则OB⊥BP,在利用已知条件可证明△OBC∽△OPB,由相似三角形的性质可得OB,OC,OP的比例式,把已知数据代入可求出OC的长,进而可求出AC的长.
解答:解:连接OB,
∵PB切⊙O于点B,
∴OB⊥BP,
∴∠OBP=90°,
∵BC⊥PO于点C,
∴∠OBC=90°,
∵∠O=∠O,
∴△OBC∽△OPB,
∴OB:OP=OC:OB,
即OB2=OC×OP,
∵OA=6,OP=8,
∴OC=
,
∴AC=OA-OC=6-
=
,
故答案为:
.
∵PB切⊙O于点B,
∴OB⊥BP,

∴∠OBP=90°,
∵BC⊥PO于点C,
∴∠OBC=90°,
∵∠O=∠O,
∴△OBC∽△OPB,
∴OB:OP=OC:OB,
即OB2=OC×OP,
∵OA=6,OP=8,
∴OC=
| 18 |
| 5 |
∴AC=OA-OC=6-
| 18 |
| 5 |
| 12 |
| 5 |
故答案为:
| 12 |
| 5 |
点评:本题考查了切线的性质、相似三角形的判定和性质,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
下列命题是假命题的是( )
| A、内错角相等 |
| B、等角的补角相等 |
| C、对顶角相等 |
| D、等腰三角形底角相等 |
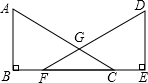 已知:如图,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:∠ACB=∠DFE.
已知:如图,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:∠ACB=∠DFE. 如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于
如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于