题目内容
 如图⊙C半径为1,圆心坐标为(3,4),点P(m,n)是⊙C内或⊙C上的一个动点,则m2+n2的最小值是
如图⊙C半径为1,圆心坐标为(3,4),点P(m,n)是⊙C内或⊙C上的一个动点,则m2+n2的最小值是
- A.9
- B.16
- C.25
- D.36
B
分析:由于圆心C的坐标为(3,4),点P的坐标为(m,n),利用勾股定理可计算出OC= =5,OP=
=5,OP= ,这样把m2+n2理解为点P点圆点的距离的平方,利用图形可得到当点运动到线段OC上时,点P离圆点最近,即m2+n2有最小值,然后求出此时的PC长即可.
,这样把m2+n2理解为点P点圆点的距离的平方,利用图形可得到当点运动到线段OC上时,点P离圆点最近,即m2+n2有最小值,然后求出此时的PC长即可.
解答:连OC交⊙O于P′点,如图,
 ∵圆心C的坐标为(3,4),点P的坐标为(m,n),
∵圆心C的坐标为(3,4),点P的坐标为(m,n),
∴OC= =5,OP=
=5,OP= ,
,
∴m2+n2是点P点圆点的距离的平方,
∴当点运动到线段OC上时,即P′处,点P离圆点最近,即m2+n2有最小值,
此时OP=OC-PC=5-1=4,则m2+n2=16.
故选B.
点评:本题考查了点与圆的位置关系:设点到圆心的距离为d,圆的半径为R,当d>R,点在圆外;当d=R,点在圆上;当d<R,点在圆内.也考查了勾股定理以及坐标与图形的关系.
分析:由于圆心C的坐标为(3,4),点P的坐标为(m,n),利用勾股定理可计算出OC=
 =5,OP=
=5,OP= ,这样把m2+n2理解为点P点圆点的距离的平方,利用图形可得到当点运动到线段OC上时,点P离圆点最近,即m2+n2有最小值,然后求出此时的PC长即可.
,这样把m2+n2理解为点P点圆点的距离的平方,利用图形可得到当点运动到线段OC上时,点P离圆点最近,即m2+n2有最小值,然后求出此时的PC长即可.解答:连OC交⊙O于P′点,如图,
 ∵圆心C的坐标为(3,4),点P的坐标为(m,n),
∵圆心C的坐标为(3,4),点P的坐标为(m,n),∴OC=
 =5,OP=
=5,OP= ,
,∴m2+n2是点P点圆点的距离的平方,
∴当点运动到线段OC上时,即P′处,点P离圆点最近,即m2+n2有最小值,
此时OP=OC-PC=5-1=4,则m2+n2=16.
故选B.
点评:本题考查了点与圆的位置关系:设点到圆心的距离为d,圆的半径为R,当d>R,点在圆外;当d=R,点在圆上;当d<R,点在圆内.也考查了勾股定理以及坐标与图形的关系.

练习册系列答案
相关题目
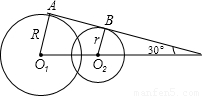
如图半径为R和r(R>r)的圆O1与圆O2相交,公切线AB与连心线的夹角为30°,则公切线AB的长为( )


A、
| ||||
B、
| ||||
C、
| ||||
| D、2(R-r) |
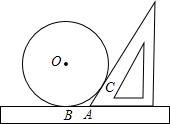 已知如图:为测量一个圆的半径,采用了下面的方法:将圆平放在一个平面上,用一个含有30°角的三角板和一把无刻度的直尺,按图示的方式测量(此时,⊙O与三角板和直尺分别相切,切点分别为点C、点B),若量得AB=5cm,试求圆的半径以及
已知如图:为测量一个圆的半径,采用了下面的方法:将圆平放在一个平面上,用一个含有30°角的三角板和一把无刻度的直尺,按图示的方式测量(此时,⊙O与三角板和直尺分别相切,切点分别为点C、点B),若量得AB=5cm,试求圆的半径以及
 已知如图:为测量一个圆的半径,采用了下面的方法:将圆平放在一个平面上,用一个含有30°角的三角板和一把无刻度的直尺,按图示的方式测量(此时,⊙O与三角板和直尺分别相切,切点分别为点C、点B),若量得AB=5cm,试求圆的半径以及
已知如图:为测量一个圆的半径,采用了下面的方法:将圆平放在一个平面上,用一个含有30°角的三角板和一把无刻度的直尺,按图示的方式测量(此时,⊙O与三角板和直尺分别相切,切点分别为点C、点B),若量得AB=5cm,试求圆的半径以及 的弧长.
的弧长. 的弧长.
的弧长.
 (R-r)
(R-r)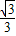 (R-r)
(R-r)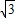 (R-r)
(R-r)