Question

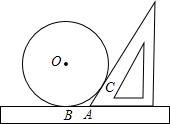已知如图：为测量一个圆的半径，采用了下面的方法：将圆平放在一个平面上，用一个含有30°角的三角板和一把无刻度的直尺，按图示的方式测量（此时，⊙O与三角板和直尺分别相切，切点分别为点C、点B），若量得AB=5cm，试求圆的半径以及

BC

的弧长．

Answer 1

分析：点O圆心，点B、C切点，连接OB，OA，OC，由邻补角的概念得到∠BAC=180°-60°=120°，由AB是切线得∠OBA=∠OCA=90°，由切线长定理知，AB=AC可证明△OBA≌△OCA，从而由全等三角形的性质求得AF的值．

解答：解：如图，连接OB，OA，OC，
则∠BAC=180°-60°=120°∠OBA=∠OCA=90°，
∵AB=AC
∴△OBA≌△OCA
∴∠BAO=

1

2

∠BAC=60°，
OB=AB•tan60°=5

3

．
由以上可得∠BOA=∠COA=30°，
∴∠BOC=60°，
∴

BC

=2×5

3

π×

60

360

=

5

3

3

π，
所以圆的半径以及

BC

的弧长分别为：5

3

，

5

3

3

π．

点评：本题利用了切线的性质，全等三角形的判定和性质，直角三角形的性质求解．