题目内容
如图半径为R和r(R>r)的圆O1与圆O2相交,公切线AB与连心线的夹角为30°,则公切线AB的长为( )


A、
| ||||
B、
| ||||
C、
| ||||
| D、2(R-r) |
分析:作O2C⊥O1A于点C.易证ABO2C为矩形,则AB=CO2.在△CO1O2中,CO1=R-r,∠CO2O1=∠P=30°,运用三角函数求CO2.
解答: 解:作O2C⊥O1A于点C.
解:作O2C⊥O1A于点C.
∵AB是切线,
∴O1A⊥AB,O2B⊥AB.
又O2C⊥O1A,
∴ABO2C为矩形,AB=CO2.
∵CO2∥AB,
∴∠CO2O1=∠P=30°,
又CO1=R-r,
∴CO2=CO1•cot30°=
(R-r).
故选C.
 解:作O2C⊥O1A于点C.
解:作O2C⊥O1A于点C.∵AB是切线,
∴O1A⊥AB,O2B⊥AB.
又O2C⊥O1A,
∴ABO2C为矩形,AB=CO2.
∵CO2∥AB,
∴∠CO2O1=∠P=30°,
又CO1=R-r,
∴CO2=CO1•cot30°=
| 3 |
故选C.
点评:此题考查了切线的性质及解直角三角形,难度中等.

练习册系列答案
相关题目
 19、如图,⊙O1和⊙O2的半径为1和3,连接O1O2,交⊙O2于点P,O1O2=8,若将⊙O1绕点P按顺时针方向旋转360°,则⊙O1与⊙O2共相切
19、如图,⊙O1和⊙O2的半径为1和3,连接O1O2,交⊙O2于点P,O1O2=8,若将⊙O1绕点P按顺时针方向旋转360°,则⊙O1与⊙O2共相切
 (R-r)
(R-r) (R-r)
(R-r) (R-r)
(R-r)
 (R-r)
(R-r) (R-r)
(R-r) (R-r)
(R-r)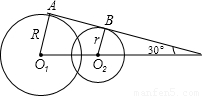
 (R-r)
(R-r)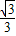 (R-r)
(R-r)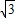 (R-r)
(R-r)