Question

7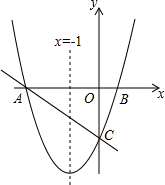．如图，对称轴为直线x=-1的抛物线y=x²+bx+c与x轴相交于A、B两点，其中点A的坐标为（-3，0）．
（1）求抛物线的解析式；
（2）C为抛物线与y轴的交点，若点P在抛物线上，且S_△POC=4S_△BOC，求点P的坐标．

Answer 1

分析 （1）根据A、B关于对称轴对称，可得B点坐标，根据待定系数法，可得答案；
（2）根据S_△POC=4S_△BOC，可得P到OC的距离是OB的4倍，可得P点的横坐标，根据自变量与函数值的对应关系，可得答案．

解答 解：（1）由A、B关于对称轴对称，
得B（1，0）．
将A、B点坐标代入函数解析式，得$\left\{\begin{array}{l}{9-3b+c=0}\\{1+b+c=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{b=2}\\{c=-3}\end{array}\right.$，
抛物线的解析式y=x²+2x-3；
（2）由S_△POC=4S_△BOC，得P到OC的距离是OB的4倍，
即P点的横坐标为4或-4，
当x=4时，y=4²+2×4-3=21，P₁（4，21）
当x=-4时，y=（-4）²+2×（-4）-3=5，即P₂（-4，5），
综上所述：P₁（4，21），P₂（-4，5）．

点评 本题考查了待定系数法求二次函数解析式，（1）利用对称性得出B点坐标是解题关键，又利用待定系数法求函数解析式；（2）利用S_△POC=4S_△BOC得P到OC的距离是OB的4倍是解题关键．