题目内容
如图所示,过点F(0,1)的直线y=kx+b与抛物线y= x2交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2>0).
x2交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2>0).(1)求b的值.
(2)求x1•x2的值.
(3)分别过M,N作直线l:y=-1的垂线,垂足分别是 M1和N1.判断△M1FN1的形状,并证明你的结论.
(4)对于过点F的任意直线MN,是否存在一条定直线m(m是常数),使m与以MN为直径的圆相切?如果有,请求出这条直线m的解析式;如果没有,请说明理由.

【答案】分析:(1)把点F的坐标代入直线可以确定b的值.
(2)联立直线与抛物线,代入(1)中求出的b值,利用根与系数的关系可以求出x1•x2的值.
(3)确定M1,N1的坐标,利用两点间的距离公式,分别求出M1F2,N1F2,M1N12,然后用勾股定理判断三角形的形状.
(4)根据题意可知y=-1总与该圆相切.
解答:解:(1)∵直线y=kx+b过点F(0,1),
∴b=1;
(2)∵直线y=kx+b与抛物线y= x2交于M(x1,y1)和N(x2,y2)两点,
x2交于M(x1,y1)和N(x2,y2)两点,
∴可以得出:kx+b= x2,
x2,
整理得: x2-kx-1=0,
x2-kx-1=0,
∵a= ,c=-1,
,c=-1,
∴x1•x2=-4,
(3)△M1FN1是直角三角形(F点是直角顶点).
理由如下:设直线l与y轴的交点是F1,
FM12=FF12+M1F12=x12+4,
FN12=FF12+F1N12=x22+4,
M1N12=(x2-x1)2=x12+x22-2x1x2=x12+x22+8,
∴FM12+FN12=M1N12,
∴△M1FN1是以F点为直角顶点的直角三角形.
 (4)符合条件的定直线m即为直线l:y=-1.
(4)符合条件的定直线m即为直线l:y=-1.
过M作MH⊥NN1于H,MN2=MH2+NH2=(x1-x2)2+(y1-y2)2,
=(x1-x2)2+[(kx1+1)-(kx2+1)]2,
=(x1-x2)2+k2(x1-x2)2,
=(k2+1)(x1-x2)2,
=(k2+1)[(x1+x2)2-4x1•x2]
=(k2+1)(16k2+16)
=16(k2+1)2,
∴MN=4(k2+1),
分别取MN和M1N1的中点P,P1,
PP1= (MM1+NN1)=
(MM1+NN1)= (y1+1+y2+1)=
(y1+1+y2+1)= (y1+y2+2)=
(y1+y2+2)= (y1+y2)+1=
(y1+y2)+1= k(x1+x2)+2=2k2+2,
k(x1+x2)+2=2k2+2,
∴PP1= MN
MN
即线段MN的中点到直线l的距离等于MN长度的一半.
∴以MN为直径的圆与l相切.
即对于过点F的任意直线MN,存在一条定直线m,使m与以MN为直径的圆相切,这条直线m的解析式是y=-1.
点评:本题考查的是二次函数的综合题,
(1)由点F的坐标求出b的值.
(2)结合直线与抛物线的解析式,利用根与系数的关系求出代数式的值.
(3)用两点间的距离公式,判断三角形的形状.
(4)根据点与圆的位置判断直线与圆的位置.
(2)联立直线与抛物线,代入(1)中求出的b值,利用根与系数的关系可以求出x1•x2的值.
(3)确定M1,N1的坐标,利用两点间的距离公式,分别求出M1F2,N1F2,M1N12,然后用勾股定理判断三角形的形状.
(4)根据题意可知y=-1总与该圆相切.
解答:解:(1)∵直线y=kx+b过点F(0,1),
∴b=1;
(2)∵直线y=kx+b与抛物线y=
 x2交于M(x1,y1)和N(x2,y2)两点,
x2交于M(x1,y1)和N(x2,y2)两点,∴可以得出:kx+b=
 x2,
x2,整理得:
 x2-kx-1=0,
x2-kx-1=0,∵a=
 ,c=-1,
,c=-1,∴x1•x2=-4,
(3)△M1FN1是直角三角形(F点是直角顶点).
理由如下:设直线l与y轴的交点是F1,
FM12=FF12+M1F12=x12+4,
FN12=FF12+F1N12=x22+4,
M1N12=(x2-x1)2=x12+x22-2x1x2=x12+x22+8,
∴FM12+FN12=M1N12,
∴△M1FN1是以F点为直角顶点的直角三角形.
 (4)符合条件的定直线m即为直线l:y=-1.
(4)符合条件的定直线m即为直线l:y=-1.过M作MH⊥NN1于H,MN2=MH2+NH2=(x1-x2)2+(y1-y2)2,
=(x1-x2)2+[(kx1+1)-(kx2+1)]2,
=(x1-x2)2+k2(x1-x2)2,
=(k2+1)(x1-x2)2,
=(k2+1)[(x1+x2)2-4x1•x2]
=(k2+1)(16k2+16)
=16(k2+1)2,
∴MN=4(k2+1),
分别取MN和M1N1的中点P,P1,
PP1=
 (MM1+NN1)=
(MM1+NN1)= (y1+1+y2+1)=
(y1+1+y2+1)= (y1+y2+2)=
(y1+y2+2)= (y1+y2)+1=
(y1+y2)+1= k(x1+x2)+2=2k2+2,
k(x1+x2)+2=2k2+2,∴PP1=
 MN
MN即线段MN的中点到直线l的距离等于MN长度的一半.
∴以MN为直径的圆与l相切.
即对于过点F的任意直线MN,存在一条定直线m,使m与以MN为直径的圆相切,这条直线m的解析式是y=-1.
点评:本题考查的是二次函数的综合题,
(1)由点F的坐标求出b的值.
(2)结合直线与抛物线的解析式,利用根与系数的关系求出代数式的值.
(3)用两点间的距离公式,判断三角形的形状.
(4)根据点与圆的位置判断直线与圆的位置.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 4、如图所示,过点P画直线a的平行线b的作法的依据是( )
4、如图所示,过点P画直线a的平行线b的作法的依据是( ) 两点.
两点.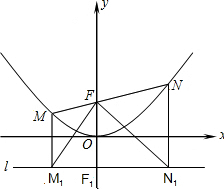 如图所示,过点F(0,1)的直线y=kx+b与抛物线y=
如图所示,过点F(0,1)的直线y=kx+b与抛物线y= 如图所示,过点D分别作DE∥BC,交AC于E,作DF∥AB,交BC于F,若AD:DC=1:2,则△ADE,△DCF,平行四边形DEBF的面积比是( )
如图所示,过点D分别作DE∥BC,交AC于E,作DF∥AB,交BC于F,若AD:DC=1:2,则△ADE,△DCF,平行四边形DEBF的面积比是( ) 如图所示,过点A(1,0)作垂直x轴的直线l,分别交函数y1=x(x≥0),y2=
如图所示,过点A(1,0)作垂直x轴的直线l,分别交函数y1=x(x≥0),y2=