Question

2．一个边长为4的等边三角形ABC的高与⊙O的直径相等，如图放置，⊙O与BC相切于点C，⊙O与AC相交于点E，
（1）求等边三角形的高；
（2）求CE的长度；
（3）若将等边三角形ABC绕点C顺时针旋转，旋转角为α（0°＜α＜360°），求α为多少时，等边三角形的边所在的直线与圆相切．

Answer 1

分析 （1）作AM⊥MC于M，在Rt△ACM中，利用勾股定理即可解决问题．
（2）连接EF，在Rt△CEF中，利用勾股定理即可解决问题．
（3）画出图形即可解决问题．

解答 解：（1）如图，作AM⊥MC于M．
∵△ABC是等边三角形，
∴∠MAC=∠MAB=30°，
∴CM=$\frac{1}{2}$AC=2，
∴AM=$\sqrt{A{C}^{2}-C{M}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$．

（2）∵CF是⊙O直径，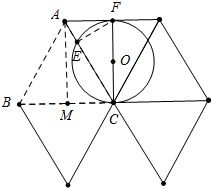
∴CF=CM=2$\sqrt{3}$，连接EF，则∠CEF=90°，
∵∠ECF=90°-∠ACB=30°，
∴EF=$\frac{1}{2}$CF=$\sqrt{3}$，
∴CE=$\sqrt{C{F}^{2}-E{F}^{2}}$=$\sqrt{（2\sqrt{3}）^{2}-（\sqrt{3}）^{2}}$=3．

（3）由图象可知，α=60°或120°或180°或300°时，等边三角形的边所在的直线与圆相切．

点评 本题考查切线的性质、等边三角形的性质、旋转变换等知识，解题的关键是灵活应用勾股定理，直角三角形30度角性质解决问题，学会画图解决旋转角度问题，属于中考常考题型．