Question

17．?ABCD中，∠BAD的平分线交直线BC于点E，线DC于点F
（1）求证：CE=CF；
（2）若∠ABC=120°，FG∥CE，FG=CE，求∠BDG．

Answer 1

分析 （1）由角平分线的定义得出∠BAE=∠DAE，由平行四边形的性质得出∠CEF=∠DAF，∠CFE=∠BAE，得出∠CEF=∠CFE，即可得出结论；
（2）连接EG，CG，先证明四边形ECFG为菱形，得出∠CFG=60°，△CFG为等边三角形，再证明△DGF≌△BGC，得出BG=DG，∠BGC=∠DGF，得出∠BGD=∠CGF=60°，证出△BDG为等边三角形，即可得出结论．

解答 证明：（1）∵AF平分∠BAD，
∴∠BAE=∠DAE，
又AB∥BC，
∴∠CEF=∠DAF，
∵AB∥CD，
∴∠CFE=∠BAE，
∴∠CEF=∠CFE，
∴CE=CF；
（2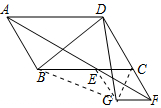）连接EG，BG，CG，如图所示：
∵AB∥CD，
∴∠ECF=∠ABC=120°，∠BAD=60°，
∴∠DAF=30°，
∵FG∥CE，FG=CE，
∴四边形ECFG是平行四边形，
∵CE=CF，
∴四边形ECFG为菱形，
∴∠CFG=60°，∠CFE=30°=∠DAF，∠ECG=∠FCG=60°，△CFG为等边三角形，
∴CG=GF，∠BCG=∠DFG=60°，AD=FD=BC，
在△DGF和△BGC中，$\left\{\begin{array}{l}{FD=BC}&{\;}\\{∠DFG=∠BCG=60°}&{\;}\\{GF=CG}&{\;}\end{array}\right.$，
∴△DGF≌△BGC（SAS），
∴BG=DG，∠BGC=∠DGF，
∴∠BGD=∠CGF=60°，
∴△BDG为等边三角形，
∴∠BDG=60°．

点评 本题考查了平行四边形的性质、全等三角形的判定与性质、等边三角形的判定与性质、菱形的判定与性质；熟练掌握平行四边形的性质，并能进行推理论证是解决问题的关键．