Question

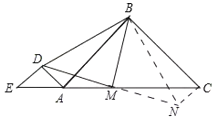
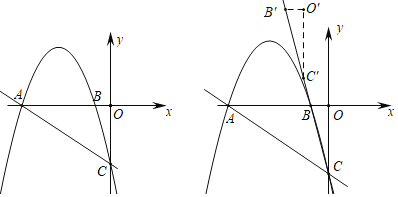
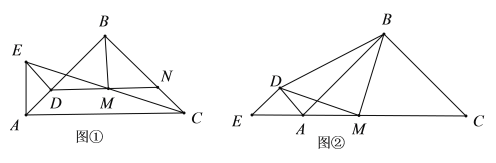
【题目】如图①，已知点在线段上，在和中，，，

，且为的中点.

（1）连接并延长交于，求证：；

（2）直接写出线段与的关系： ；

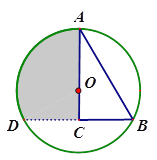
（3）若将绕点逆时针旋转，使点在线段的延长线上（如图②所示位置），则（2）中的结论是否仍成立？若成立，请证明；若不成立，请说明理由.

Answer 1

【答案】（1）见解析；（2），；（3）成立，证明见解析；

【解析】

（1）由∠ABC＝∠ADE＝90°可推出DE∥BC，再根据平行线的性质，推出∠DEM＝∠MCN，根据ASA证明△EMD≌△CMN，求出CN＝ED，即可得到CN＝AD；

（2）由（1）可知CN＝AD，DM＝MN，再由AB＝BC，可得BD＝BN，从而可得△DBN是等腰直角三角形，且BM是底边DN上的中线，即可得到，BM⊥DM；

（3）作CN∥DE交DM的延长线于N，连接BN，根据平行线的性质求出∠EDM＝∠CNM，利用AAS证明△EMD≌△CMN，得到CN＝DE＝DA，MN＝MD，∠E＝∠NCM＝45°，然后根据SAS证△DBA≌△NBC，推出△DBN是等腰直角三角形，且BM是底边的中线，根据等腰直角三角形的性质即可进行证明．

解：（1）∵AD＝DE，AB＝BC，，

∴△ABC和△ADE为等腰直角三角形，，

∴DE∥BC，

∴∠DEM＝∠NCM，

在△EMD和△CMN中，，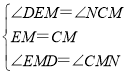

∴△EMD≌△CMN（ASA），

∴CN＝DE，

∵AD＝DE，

∴CN＝AD；

（2），BM⊥DM，

理由：由（1）得：△EMD≌△CMN，

∴CN＝AD，DM＝MN，

∵BA＝BC，

∴BD＝BN，

∴△DBN是等腰直角三角形，且BM是底边的中线，

∴，BM⊥DM；

（3），BM⊥DM仍成立，

证明：如图，作CN∥DE交DM的延长线于N，连接BN，

∴∠EDM＝∠CNM，

在△EMD与△CMN中，，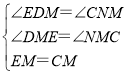

∴△EMD≌△CMN（AAS），

∴CN＝DE＝DA，MN＝MD，∠E＝∠NCM＝45°，

又∵∠DAB＝180°∠DAE∠BAC＝90°，∠BCN＝∠BCM＋∠NCM＝45°＋45°＝90°，

∴∠DAB＝∠BCN，

在△DBA和△NBC中，，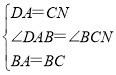

∴△DBA≌△NBC（SAS），

∴∠DBA＝∠NBC，DB＝BN，

∴∠DBN＝∠ABC＝90°，

∴△DBN是等腰直角三角形，且BM是底边的中线，

∴，BM⊥DM．