题目内容
已知abc≠0,且abc≠1,x,y,z为非零整数,且x+y+z=0,ayz=bxz=cxy,求证:abc=-1.
考点:幂的乘方与积的乘方,同底数幂的乘法
专题:证明题
分析:根据ayz=bxz=cxy,得出ay=bx,az=cx,bz=cy,然后求出x、y、z之间的关系,最后得出(abc)x=1,即可证明abc=-1.
解答:解:∵ayz=bxz=cxy,
∴ay=bx①,
az=cx②,
bz=cy③,
①×②得:ay+z=(bc)x,
∵x+y+z=0,
∴y+z=-x,
则a-x=(bc)x,
即(abc)x=1,
∵x为非0整数,
∴abc=1,或abc=-1,
∵abc≠1,
∴abc=-1.
∴ay=bx①,
az=cx②,
bz=cy③,
①×②得:ay+z=(bc)x,
∵x+y+z=0,
∴y+z=-x,
则a-x=(bc)x,
即(abc)x=1,
∵x为非0整数,
∴abc=1,或abc=-1,
∵abc≠1,
∴abc=-1.
点评:本题考查了积得乘方和幂的乘方,解答本题的关键是根据题意,求出z、y、z之间的关系,难度一般.

练习册系列答案
相关题目
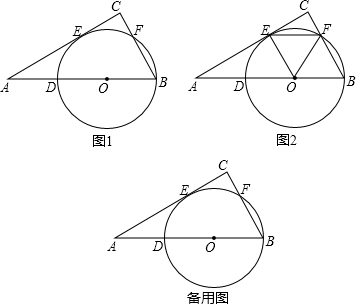 如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.