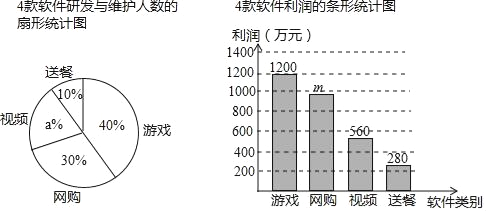
题目内容
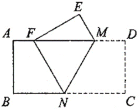
【题目】如图,矩形ABCD中,点M、N分别在AD、BC边上,将矩形ABCD沿MN翻折,点C恰好落在AD边上的点F处,若MD=1,∠MNC=60°,则AB的长为_____.
【答案】![]()
【解析】
由翻折变换可得EF=CD,MD=EM=1,∠MNC=∠FNM=60°,∠C=∠EFN=90°,由平行线的性质可得∠FMN=∠MNC=60°,即可求∠EFM=30°,由直角三角形的性质可求解.
解:∵将矩形ABCD沿MN翻折,点C恰好落在AD边上的点F处.
∴EF=CD,MD=EM=1,∠MNC=∠FNM=60°,∠C=∠EFN=90°
∵AD∥BC,
∴∠FMN=∠MNC=60°,
∴∠MFN=60°,
∴∠EFM=30°,且∠E=90°,
∴EF=![]() EM=
EM=![]() ,
,
∴AB=CD=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目