题目内容
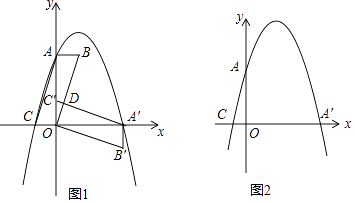
【题目】如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )

A. ①②③ B. ①③④ C. ①④ D. ①②④
【答案】C
【解析】
根据三角形内角和定理以及三角形角平分线的定义可得∠BOC=90°+![]() ∠1,再结合三角形外角性质可得∠ECD=∠OBC+∠2,从而可得∠BOC=90°+∠2,据此即可进行判断.
∠1,再结合三角形外角性质可得∠ECD=∠OBC+∠2,从而可得∠BOC=90°+∠2,据此即可进行判断.
∵BO,CO分别平分∠ABC,∠ACB,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∵∠ABC+∠ACB+∠1=180°,
∴∠ABC+∠ACB=180°-∠1,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠1)=90°-
(180°-∠1)=90°-![]() ∠1,
∠1,
∴∠BOC=180°-∠OBC-∠OCB=180°-(90°-![]() ∠1)=90°+
∠1)=90°+![]() ∠1,
∠1,
∵∠ACD=∠ABC+∠1,CE平分∠ACD,
∴∠ECD=![]() ∠ACD=
∠ACD=![]() (∠ABC+∠1),
(∠ABC+∠1),
∵∠ECD=∠OBC+∠2,
∴∠2=![]() ∠1,即∠1=2∠2,
∠1,即∠1=2∠2,
∴∠BOC=90°+![]() ∠1=90°+∠2,
∠1=90°+∠2,
∴①④正确,②③错误,
故选C.

练习册系列答案
相关题目