题目内容
如图，
是
的直径，
是
的中点，
的切线
交
的延长线于点
，
是
的中点，
的延长线交切线
于点
，
交
于点
，连接
.
（1）求证：
；
（2）若
，求
的长.
(1)证明见解析
(2)
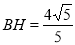
【解析】
试题分析：(1)连接OC，若要证明C为AD的中点，只需证OC//BD，已知C是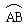
的中点，可知OC⊥AB，又BD是切线，可知BD⊥AB，问题得证
(2)由（1）及E为OB中点可知△COE≌△FBE，从而可知BF=CO=BO=2，由勾股定理可得AF的长，由面积法即可求出BH的长
试题解析：（1）连接OC
∵C是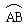的中点，AB是⊙O的直径
∴OC⊥AB
∵BD是⊙O的切线
∴BD⊥AB
∴OC//BD
∵AO=BO
∴AC=CD
（2）∵E是OB的中点
∴OE=BE
在△COE和△FBE中
∴△COE≌△FBE（ASA)
∴BF=CO
∵OB=2
∴BF=2
∴AF=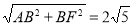
∵AB是直径
∴BH⊥AF
考点：1、平行线分线段成比例定理；2、切线的性质；3勾股定理；4、全等三角形
练习册系列答案
相关题目
