题目内容
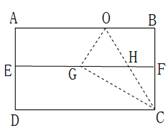
 将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若AB:BC=4:5,则cos∠AFE的值为
将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若AB:BC=4:5,则cos∠AFE的值为
- A.4:5
- B.3:5
- C.3:4
- D.

D
分析:cos∠AFE=sin∠CFD=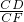 ,根据折叠的定义可以得到CB=CF,则
,根据折叠的定义可以得到CB=CF,则 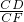 =
= ,即可求出sin∠CFD的值,继而可得出答案.
,即可求出sin∠CFD的值,继而可得出答案.
解答:∵∠AFE+∠CFD=90°,
∴cos∠AFE=sin∠CFD=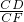 ,
,
由折叠可知,CB=CF,
矩形ABCD中,AB=CD,sin∠CFD= =
= .
.
故选D.
点评:本题考查折叠变换的性质及锐角三角函数的定义,检测学生灵活运用知识的能力.
分析:cos∠AFE=sin∠CFD=
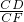 ,根据折叠的定义可以得到CB=CF,则
,根据折叠的定义可以得到CB=CF,则 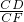 =
= ,即可求出sin∠CFD的值,继而可得出答案.
,即可求出sin∠CFD的值,继而可得出答案.解答:∵∠AFE+∠CFD=90°,
∴cos∠AFE=sin∠CFD=
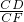 ,
,由折叠可知,CB=CF,
矩形ABCD中,AB=CD,sin∠CFD=
 =
= .
.故选D.
点评:本题考查折叠变换的性质及锐角三角函数的定义,检测学生灵活运用知识的能力.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若AB:BC=4:5,则cos∠AFE的值为( )
将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若AB:BC=4:5,则cos∠AFE的值为( )| A、4:5 | ||
| B、3:5 | ||
| C、3:4 | ||
D、
|
 22、用尺轨三等分任意角是数学中的一大难题,但我们可以用“折纸法”把一个直角三等分.如图所示,
22、用尺轨三等分任意角是数学中的一大难题,但我们可以用“折纸法”把一个直角三等分.如图所示,