题目内容

5．已知关于x的方程x2-2mx+3m=0的两个实数根是x1，x2，且（x1-x2）2=1，求m的值．

分析 根据根与系数的关系得到x1+x2=2m，x1•x2=3m，由于（x1-x2）2=（x1+x2）2-4x1x2，代入方程求得答案即可．

解答 解：∵关于x的方程x2-2mx+3m=0的两个实数根是x1，x2，
∴x1+x2=2m，x1•x2=3m，
∵（x1-x2）2=（x1+x2）2-4x1x2，
∴4m2-12m=1，
解得：m=$\frac{3+\sqrt{10}}{2}$或m=$\frac{3-\sqrt{10}}{2}$．

点评 此题考查根与系数的关系，若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．

练习册系列答案
相关题目
15．在有些情况下，不需要计算出结果也能把绝对值符号去掉．例如：
|6+7|=6+7；|6-7|=7-6；|7-6|=7-6；|-6-7|=6+7；
根据上面的规律，把下列各式写成去掉绝对值符号的形式：
（1）|7-21|=21-7；
（2）|$-\frac{1}{2}+0.8$|=0.8-$\frac{1}{2}$；
（3）|$\frac{7}{17}-\frac{7}{18}$|=$\frac{7}{17}-\frac{7}{18}$；
（4）|$3.2-2.8-\frac{2}{3}$|=2.8+$\frac{2}{3}$-3.2；
（5）用合理的方法计算：|$\frac{1}{5}-\frac{150}{557}$|+|$\frac{150}{557}-\frac{1}{2}$|-|$\frac{1}{5}$$-\frac{1}{2}$|．
16．下列二次根式中，哪些是最简二次根式？把不是最简二次根式的化成最简二次根式．
（1）$\sqrt{0.2}$；
（2）$\sqrt{\frac{2}{3}ab}$；
（3）$\sqrt{{x}^{2}+1}$；
（4）$\sqrt{32m}$；
（5）$\sqrt{{a}^{3}+6{a}^{2}+9a}$（a＞0）．
13．若（m-1）2+$\sqrt{n+2}$=0，则nm的值是（　　）
A．-2B．0C．1D．2
20．一件工作，甲单独做20小时完成，甲、乙合做7.5小时完成，甲先单独做4小时，然后乙加入合作，那么两人合作还要多少小时完成？
10．定义两种运算：“⊕”、“?”，对于任意两个整数a、b，a⊕b=-a+b-2，a?b=a×b-2，求2?[（4⊕6）÷（3?5）]的值．
17．比较$\frac{\sqrt{7}-1}{3}$与$\frac{2}{3}$的大小．
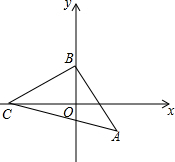12．如图，已知B（0，1），C（-2，0），过点B作AB⊥BC，使得AB=BC．
（1）求A点坐标；
（2）点P从B出发，以1个单位/秒的速度沿射线BA运动，运动时间为t秒，请用含有t的式子表示△BCP的面积S；
（3）在（2）的条件下，射线BP交x轴于点F，当x轴平分∠BCP时，CF=$\frac{5}{2}$，S=$\frac{10}{3}$，求此时t值及此时P点坐标．
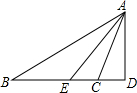13．如图，△ABC中，∠B=36°，∠ACB=110°，AE是∠BAC的平分线，AD是BC边上的高，求∠DAE的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网