题目内容
若一个三角形的三边长的平方分别为:32,42,x2则此三角形是直角三角形的x2的值是()
A.42 B.52 C.7 D.52或7
D
【解析】
试题分析:此题要考虑两种情况:x是斜边或4是斜边.根据勾股定理,即“两条直角边的平方等于斜边的平方”进行求解.
当x是斜边时,则x2=9+16=25;
当4是斜边时,则x2=16-9=7
故选D
考点:勾股定理.
考点分析: 考点1:解直角三角形 (1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边) 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 在实数范围内有意义,则
在实数范围内有意义,则 的取值范围是( )
的取值范围是( ) B、
B、 C、
C、 D、
D、
 ,则菱形较小的内角的度数为 .
,则菱形较小的内角的度数为 .
 ,b>
,b> ,则a+b的最小值是( )
,则a+b的最小值是( )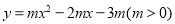 与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,且OC=OB.
与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,且OC=OB.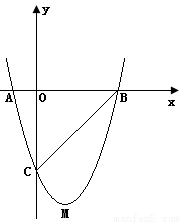

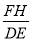 的值.
的值.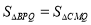 ,求P点的坐标.
,求P点的坐标.
