题目内容
16.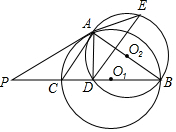 如图,⊙O1与⊙O2相交于A、B两点,AB是⊙O2的直径,过点A作⊙O1的切线交⊙O2于点E,并与BO1的延长线交于点P,BP分别与⊙O1、⊙O2交于点C、D.求证:
如图,⊙O1与⊙O2相交于A、B两点,AB是⊙O2的直径,过点A作⊙O1的切线交⊙O2于点E,并与BO1的延长线交于点P,BP分别与⊙O1、⊙O2交于点C、D.求证:(1)AC∥ED;
(2)AD=AE.
分析 (1)根据弦切角定理得到∠ACB=∠EAB,由圆周角定理得到∠EDB=∠EAB,根据平行线的判定定理证明;
(2)根据圆周角定理得到∠CAB=90°,根据平行线的性质得到AB⊥DE,根据垂径定理证明即可.
解答 证明:(1)∵AE是⊙O1的切线,
∴∠ACB=∠EAB,
由圆周角定理得,∠EDB=∠EAB,
∴∠EDB=∠ACB,
∴AC∥ED;
(2)∵BC是⊙O1的直径,
∴∠CAB=90°,
∵AC∥ED,
∴AB⊥DE,
∴$\widehat{AD}$=$\widehat{AE}$,
∴AD=AE.
点评 本题考查的是相交两圆的性质、切线的性质,掌握弦切角定理、圆周角定理和切线的性质定理是解题的关键.

练习册系列答案
相关题目
1.已知非零向量$\overrightarrow{a}$、$\overrightarrow{b}$之间满足$\overrightarrow{a}$=-3$\overrightarrow{b}$,下列判断正确的是( )
| A. | $\overrightarrow a$的模为3 | B. | $\overrightarrow a$与$\overrightarrow b$的模之比为-3:1 | ||
| C. | $\overrightarrow a$与$\overrightarrow b$平行且方向相同 | D. | $\overrightarrow a$与$\overrightarrow b$平行且方向相反 |
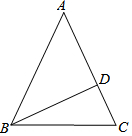 如图,在等腰△ABC中,AB=AC,BD为高.(从下列问题中任选一问作答)
如图,在等腰△ABC中,AB=AC,BD为高.(从下列问题中任选一问作答)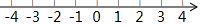 在数轴上分别画出点A、B、C、D,点A表示数$\frac{1}{3}$,点B表示数1$\frac{1}{2}$,点C表示数-2,点D表示数2$\frac{3}{4}$;并将点A、B、C、D所表示的数用“>”连接.
在数轴上分别画出点A、B、C、D,点A表示数$\frac{1}{3}$,点B表示数1$\frac{1}{2}$,点C表示数-2,点D表示数2$\frac{3}{4}$;并将点A、B、C、D所表示的数用“>”连接.