题目内容
11.某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:| x | 30 | 32 | 34 | 36 |
| y | 40 | 36 | 32 | 28 |
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
分析 (1)根据待定系数法解出解析式即可;
(2)根据题意列出方程解答即可;
(3)根据题意列出函数解析式,利用函数解析式的最值解答即可.
解答 解:(1)设该函数的表达式为y=kx+b,根据题意,得
$\left\{\begin{array}{l}{40=30k+b}\\{36=32k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=100}\end{array}\right.$.
故该函数的表达式为y=-2x+100;
(2)根据题意得,
(-2x+100)(x-30)=150,
解这个方程得,x1=35,x2=45,
故每件商品的销售价定为35元或45元时日利润为150元;
(3)根据题意,得
w=(-2x+100)(x-30)
=-2x2+160x-3000
=-2(x-40)2+200,
∵a=-2<0 则抛物线开口向下,函数有最大值,
即当x=40时,w的值最大,
∴当销售单价为40元时获得利润最大.
点评 此题考查二次函数的应用,关键是根据题意列出方程和函数解析式,利用函数解析式的最值分析.

练习册系列答案
相关题目
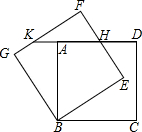 如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则AK=2$\sqrt{3}$-3.
如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则AK=2$\sqrt{3}$-3.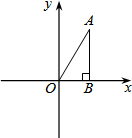 如图,△ABO中,AB⊥OB,AB=$\sqrt{3}$,OB=1,把△ABO绕点O旋转120°后,得到△A1B1O,则点A1的坐标为(-2,0)或(1,-$\sqrt{3}$).
如图,△ABO中,AB⊥OB,AB=$\sqrt{3}$,OB=1,把△ABO绕点O旋转120°后,得到△A1B1O,则点A1的坐标为(-2,0)或(1,-$\sqrt{3}$). 如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点Bn的坐标为(3×2n-2,$\sqrt{3}$×2n-2).
如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点Bn的坐标为(3×2n-2,$\sqrt{3}$×2n-2).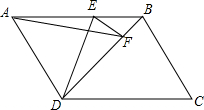 如图,在平行四边形ABCD中,AD⊥BD,点E、点F分别在AB、BD上,且AD=AE=DF,连接DE、AF、EF.
如图,在平行四边形ABCD中,AD⊥BD,点E、点F分别在AB、BD上,且AD=AE=DF,连接DE、AF、EF.