题目内容
7.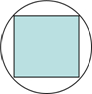 在如图的圆形纸片上做随机扎针实验,正方形是圆的内接正方形,则针头扎在圆的阴影区域内的概率为$\frac{2}{π}$.
在如图的圆形纸片上做随机扎针实验,正方形是圆的内接正方形,则针头扎在圆的阴影区域内的概率为$\frac{2}{π}$.
分析 设圆的半径为r,表示出正方形的边长为$\sqrt{2}$r,然后分别求得正方形和圆的面积,用正方形的面积除以圆的面积即可求得答案.
解答 解:设圆的半径为r,则正方形的边长为$\sqrt{2}$r,
所以针头扎在圆的阴影区域内的概率为$\frac{(\sqrt{2}r)^{2}}{π{r}^{2}}$=$\frac{2}{π}$.
故答案为:$\frac{2}{π}$.
点评 此题考查了几何概率,用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
17.已知⊙O1的半径为3cm,⊙O2的半径为5cm,圆心距O1O2为2cm,则⊙O1和⊙O2的位置关系是( )
| A. | 相交 | B. | 外离 | C. | 外切 | D. | 内切 |
18.下列说法中,正确的是( )
| A. | 若ac=bc,则a=b | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则a=b | C. | 若a2=b2,则a=b | D. | 若|a|=|b|,则a=b |
2.下列说法正确的是( )
| A. | 棱柱的侧面可以是正方形,也可以是三角形 | |
| B. | 一个几何体的表面不可能只有曲面组成 | |
| C. | 棱柱的各条棱都相等 | |
| D. | 圆锥是由平面和曲面组成的几何体 |
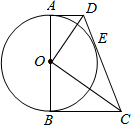 如图,在梯形ABCD中,AD∥BC,∠B=90°,以AB为直径作⊙O,恰与一边CD相切于点E,连接OD、OC.若四边形ABCD的面积是48,设OD=x,OC=y,且x+y=14;
如图,在梯形ABCD中,AD∥BC,∠B=90°,以AB为直径作⊙O,恰与一边CD相切于点E,连接OD、OC.若四边形ABCD的面积是48,设OD=x,OC=y,且x+y=14;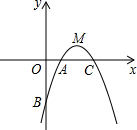 已知二次函数y=-x2+4x-3,其图象与y轴交于点B,与x轴交于A、C 两点,顶点为M.
已知二次函数y=-x2+4x-3,其图象与y轴交于点B,与x轴交于A、C 两点,顶点为M. 如图,△OAB是边长为2的等边三角形,过点A的直线$y=-\frac{\sqrt{3\;}}{3}x$+m与x轴交于点E.
如图,△OAB是边长为2的等边三角形,过点A的直线$y=-\frac{\sqrt{3\;}}{3}x$+m与x轴交于点E.