题目内容
如图，∠COD=116°，∠BOD=90°，OA平分∠BOC，求∠AOD的度数．
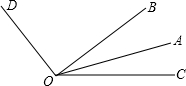
解：∵∠COD=116°，∠BOD=90°，
∴∠BOC=∠COD-∠BOD=116°-90°=26°，
又∵OA平分∠BOC，
∴∠AOB=
∠BOC=×26=13°，
∴∠AOD=∠BOD+∠AOB=90°+13°=103°．
∴∠AOD的度数是103°．
故答案为103°．
分析：由角平分线的定义，结合角的运算，易求∠AOD的度数．
点评：根据角平分线定义得出所求角与已知角的关系转化求解．
∴∠BOC=∠COD-∠BOD=116°-90°=26°，
又∵OA平分∠BOC，
∴∠AOB=
∠BOC=×26=13°，∴∠AOD=∠BOD+∠AOB=90°+13°=103°．
∴∠AOD的度数是103°．
故答案为103°．
分析：由角平分线的定义，结合角的运算，易求∠AOD的度数．
点评：根据角平分线定义得出所求角与已知角的关系转化求解．
练习册系列答案
阅读快车系列答案
相关题目
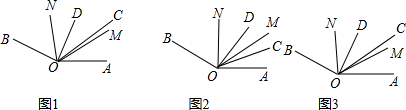
如图的扇形统计图表示的是120名同学某次体育测试的成绩，分为甲等，乙等，丙等和丁等，OA⊥OD，∠COD=54°，∠AOB=∠BOC，回答下列问题：
如图，∠AOB与∠COD都是直角，若∠BOC：∠AOD=7：11，求∠AOC的度数．
，∠COD＝60°．