题目内容
14.正方形ABCD边长为4,G是对角线AC上一动点,过点C作CF⊥BG,垂足为F,连接DF,则DF的最小值为2$\sqrt{2}$.分析 当G为AC的中点时,DF最小,此时,F与G重合,是AC与BD的交点;先根据勾股定理求出BD,即可得出DF的最小值.
解答 解:根据题意,当G为AC的中点时,DF最小,此时,F与G重合,是AC与BD的交点;
∵四边形ABCD是正方形,
∴AB=AD=4,∠BAD=90°,DF=$\frac{1}{2}$BD,
∴BD=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∴DF=$\frac{1}{2}$BD=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查了正方形的性质、勾股定理以及最小值问题;根据题意得出当G为AC的中点时,DF最小是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
4.计算(m3)2÷m3的结果等于( )
| A. | m2 | B. | m3 | C. | m4 | D. | m6 |
5.五个城市的国际标准时间(单位:时)在数轴上表示如图所示,我市2013年初中毕业学业检测与高中阶段学校招生考试于2013年6月16日上午9时开始,此时应是( 

| A. | 纽约时间2013年6月16日晚上22时 | |
| B. | 多伦多时间2013年6月15日晚上21时 | |
| C. | 伦敦时间2013年6月16日凌晨1时 | |
| D. | 汉城时间2013年6月16日上午8时 |
 如图,若三个小正方形的边长都为2,则图中阴影部分面积的和是$\frac{3π}{2}$.
如图,若三个小正方形的边长都为2,则图中阴影部分面积的和是$\frac{3π}{2}$.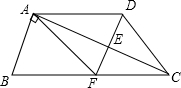 已知:如图,在梯形ABCD中,AD∥BC,BC=2AD,AC⊥AB,点E是AC的中点,DE的延长线与BC相交于点F.求证:四边形AFCD是菱形.
已知:如图,在梯形ABCD中,AD∥BC,BC=2AD,AC⊥AB,点E是AC的中点,DE的延长线与BC相交于点F.求证:四边形AFCD是菱形.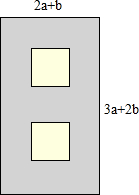 如图,在一块长为3a+2b,宽为2a+b的长方形木板中挖去两个边长为a+b的正方形,形成如图所示的“日”字形边框.
如图,在一块长为3a+2b,宽为2a+b的长方形木板中挖去两个边长为a+b的正方形,形成如图所示的“日”字形边框.