题目内容
2. 如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.(1)若BP=10m,求居民楼AB的高度;(精确到0.1,$\sqrt{3}$≈1.732)
(2)若PC=24m,求C、A之间的距离.
分析 (1)在Rt△ABP中根据tan60°=$\frac{AB}{PB}$=$\frac{AB}{10}=\sqrt{3}$,即可得到结论;
(2)过点C作CE⊥BP于点E,在Rt△PCE中,根据cos45°=$\frac{PE}{PC}$=$\frac{PE}{24}$=$\frac{\sqrt{2}}{2}$,得到PE=12$\sqrt{2}$m,于是得到AC=BE=10$\sqrt{3}$+12$\sqrt{2}$m.
解答 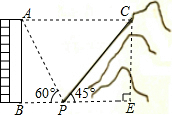 解:(1)在Rt△ABP中
解:(1)在Rt△ABP中
∵PB=10m,∠APB=60°,
∴tan60°=$\frac{AB}{PB}$=$\frac{AB}{10}=\sqrt{3}$,
∴AB=10$\sqrt{3}$≈17.3m,
答:居民楼AB的高度约为17.3;
(2)过点C作CE⊥BP于点E,在Rt△PCE中,
∵∠CPE=45°,
∴cos45°=$\frac{PE}{PC}$=$\frac{PE}{24}$=$\frac{\sqrt{2}}{2}$,
∴PE=12$\sqrt{2}$m,
∴AC=BE=10$\sqrt{3}$+12$\sqrt{2}$m,
答:C、A之间的距离约为(10$\sqrt{3}$+12$\sqrt{2}$)m.
点评 此题主要考查了解直角三角形-仰角、坡角问题的应用,要求学生借助仰角、坡角关系构造直角三角形,并结合图形利用三角函数求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.四边形ABCD中,0是对角线的交点,下列条件能判定这个四边形为正方形的是( )
| A. | AB∥CD,AB=CD,AC=BD | B. | AD∥BC,AB=CD,∠A=∠B | ||
| C. | AO=BO=CO=DO,AC⊥BD | D. | AO=CO,BO=DO,AB=BC |
 如图,点C、D是线段AB上的两点,若AC=4,CD=8,DB=3,
如图,点C、D是线段AB上的两点,若AC=4,CD=8,DB=3,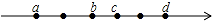 数轴上有六个点,每相邻的两个点间的距离都是1个单位长度,有理数a、b、c、d所对应的点是这些点中的4个,位置如图所示.
数轴上有六个点,每相邻的两个点间的距离都是1个单位长度,有理数a、b、c、d所对应的点是这些点中的4个,位置如图所示. 如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在外有一点F,使FA⊥AE,FC⊥BC.在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.有以下结论:①BE=CF;②ME⊥BC;③DE=DN;④图中度数为22.5°的角有5个,其中正确的结论有( )
如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在外有一点F,使FA⊥AE,FC⊥BC.在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.有以下结论:①BE=CF;②ME⊥BC;③DE=DN;④图中度数为22.5°的角有5个,其中正确的结论有( )