题目内容
7. 如图:两条宽为a的纸条,交叉重叠放在一起,且它们的交角为α,则重叠部分的面积(阴影部分)为( )
如图:两条宽为a的纸条,交叉重叠放在一起,且它们的交角为α,则重叠部分的面积(阴影部分)为( )| A. | a2sinα | B. | a2 | C. | $\frac{{a}^{2}}{sinα}$ | D. | $\frac{{a}^{2}}{cosα}$ |
分析 首先过A作AE⊥BC,AF⊥CD于F,垂足为E,F,证明四边形ABCD是菱形,利用三角函数算出BC的长,最后根据菱形的面积公式算出重叠部分的面积即可.
解答 解:如图所示:过A作AE⊥BC,AF⊥CD于F,垂足为E,F,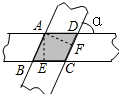
∴∠AEB=∠AFD=90°,
∵AD∥CB,AB∥CD,
∴四边形ABCD是平行四边形,
∵纸条宽度都为a,
∴AE=AF=a,
∵四边形ABCD的面积=BC•AE=CD•AF,
∴BC=CD,
∴四边形ABCD是菱形.
∴BC=AB,
∵$\frac{AE}{AB}$=sinα,
∴BC=AB=$\frac{AE}{sinα}$=$\frac{a}{sinα}$,
∴重叠部分(阴影部分)的面积为=BC×AE=$\frac{a}{sinα}$×a=$\frac{{a}^{2}}{sinα}$.
故选:C.
点评 此题主要考查了菱形的判定与性质,以及三角函数的应用;关键是证明四边形ABCD是菱形,利用三角函数求出BC的长.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
17.已知抛物线y=ax2+2x+1与x轴没有交点,那么该抛物线的顶点所在的象限是( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
18.下列四组线段中,可以构成直角三角形的是( )
| A. | 4,5,6 | B. | 6,8,10 | C. | 2,3,4 | D. | 1,1,2 |
2.若$\sqrt{{{(1-m)}^2}}$=m-1,则m的取值范围是( )
| A. | m≥1 | B. | m≤1 | C. | m=1 | D. | 一切实数 |
19.下列多项式:①x2+y2;②x2-1;③x3+4x-4;④x2-10x+25,其中能直接用公式法因式分解的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
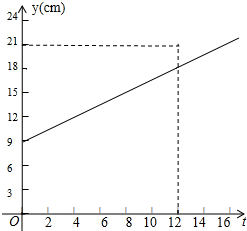 某种植物生长t天的高度为y厘米,如图反映了y与t之间的函数关系,请根据图象回答问题:
某种植物生长t天的高度为y厘米,如图反映了y与t之间的函数关系,请根据图象回答问题: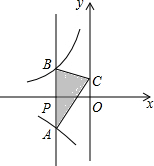 如图,过x轴负半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=$\frac{-6}{x}$,y=$\frac{4}{x}$交于A,B两点.若点C是y轴上任意一点,连接AC,BC,则△ABC的面积是5.
如图,过x轴负半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=$\frac{-6}{x}$,y=$\frac{4}{x}$交于A,B两点.若点C是y轴上任意一点,连接AC,BC,则△ABC的面积是5. 解下列不等式,并把解集在数轴上表示出来.
解下列不等式,并把解集在数轴上表示出来.