题目内容
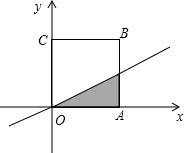 如图,边长为2的正方形OABC放置在平面直角坐标系中,OA在x轴正半轴上,OC在y轴正半轴上,当直线y=kx的系数k从0开始逐渐变大时,直线在正方形上扫过的面积为记为S,则S关于k的函数图象是( )
如图,边长为2的正方形OABC放置在平面直角坐标系中,OA在x轴正半轴上,OC在y轴正半轴上,当直线y=kx的系数k从0开始逐渐变大时,直线在正方形上扫过的面积为记为S,则S关于k的函数图象是( )分析:由于直线OB的解析式为y=x,该直线的斜率k=1,所以分两种情况进行讨论:①0≤k≤1;②k>1,针对每一种情况分别求出S,然后根据自变量和函数值的取值范围运用排除法求解即可.
解答: 解:∵B(2,2),
解:∵B(2,2),
∴直线OB的解析式为y=x,其中k=1.
①当0≤k≤1时,直线y=kx与AB相交,设交点为D,则D(2,2k).
S=S△OAD=
•OA•AD=
×2×2k=2k;
此时,它的函数图象为一条线段,故排除C、D;
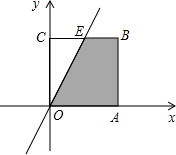
②当k>1时,直线y=kx与BC相交,设交点为E,则E(
,2).
S=S梯形OABE=
(EB+OA)•AB=
(2-
+2)×2=4-
,
 ∵k>1,
∵k>1,
∴S随k的增大而增大,且S无限接近于4,但永远不可能等于4,故排除A.
故选B.
 解:∵B(2,2),
解:∵B(2,2),∴直线OB的解析式为y=x,其中k=1.
①当0≤k≤1时,直线y=kx与AB相交,设交点为D,则D(2,2k).
S=S△OAD=
| 1 |
| 2 |
| 1 |
| 2 |
此时,它的函数图象为一条线段,故排除C、D;
②当k>1时,直线y=kx与BC相交,设交点为E,则E(
| 2 |
| k |
S=S梯形OABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| k |
| 2 |
| k |
 ∵k>1,
∵k>1,∴S随k的增大而增大,且S无限接近于4,但永远不可能等于4,故排除A.
故选B.
点评:本题考查了运用分类讨论的思想求动点的函数图象的问题:分别求出每个时段的函数关系式,然后根据自变量和函数值的取值范围进行判断.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目

 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P. 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
