题目内容
4. 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则BG的长( )
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则BG的长( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
分析 根据线段中点的定义求出DE=EC=3,再根据翻折变换的性质可得EF=DE,AF=AD,然后利用“HL”证明Rt△ABG和Rt△AFG全等,根据全等三角形对应边相等可得BG=FG,设BG=x,然后表示出CG、EG,再利用勾股定理列方程求解即可.
解答 解:∵E是边CD的中点,正方形ABCD的边长为6,
∴DE=EC=3,
∵△ADE沿AE对折至△AFE,
∴EF=DE=3,AF=AD=6,
∴AB=AF=6,
在Rt△ABG和Rt△AFG中,$\left\{\begin{array}{l}{AG=AG}\\{AB=AF}\end{array}\right.$,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=FG,
设BG=x,则CG=6-x,EG=3+x,
在Rt△CGE中,由勾股定理得,CG2+EC2=EG2,
即(6-x)2+32=(3+x)2,
解得x=2,
即BG=2.
故选B.
点评 本题考查了翻折变换的性质,正方形的性质,勾股定理,全等三角形的判定与性质,此类题目,要注意翻折变换前后的对应角和对应边分别相等,本题关键在于最后利用勾股定理列出方程.

练习册系列答案
相关题目
14.某批发店将进价为4元的小商品按5元卖出时,可卖出500件,已知这种商品每件涨价1元,其销售量就减少10件,若要赚得5600元利润,售价应定为( )
| A. | 20元 | B. | 39元 | C. | 20元或39元 | D. | 50元 |
15.要使分式$\frac{1}{2-x}$有意义,则x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≠-2 | D. | x≠2 |
12.下列各式中,一定为二次根式的是( )
| A. | $\sqrt{-5}$ | B. | $\root{3}{m}$ | C. | $\sqrt{2m}$ | D. | $\sqrt{{m}^{2}+1}$ |
19.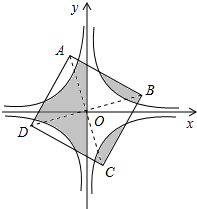 在平面直角坐标系中,有反比例函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的图象和正方形ABCD,原点O与对角线AC,BD的交点重合,且如图所示的阴影部分面积为8,则AB的长是( )
在平面直角坐标系中,有反比例函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的图象和正方形ABCD,原点O与对角线AC,BD的交点重合,且如图所示的阴影部分面积为8,则AB的长是( )
 在平面直角坐标系中,有反比例函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的图象和正方形ABCD,原点O与对角线AC,BD的交点重合,且如图所示的阴影部分面积为8,则AB的长是( )
在平面直角坐标系中,有反比例函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的图象和正方形ABCD,原点O与对角线AC,BD的交点重合,且如图所示的阴影部分面积为8,则AB的长是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
9.16的算术平方根是( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4?? |
16.若(am+1bn+2)(a2n-1b2m)=a3b5,则m+n的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | -3 |