题目内容
16．学校政教处组织65名七年级学生为一次大型讲座会场搬椅子，A组学生每人搬6把椅子，其它组学生每人搬8把椅子，总共搬了400把椅子，问A组学生有多少人参加搬椅子？分析：设A组同学有x人参加搬椅子，列表如下| 参加年级 | A组学生 | 其它组学生 | 总数 |
| 参加人数 | x | 65-x | 65 |
| 每人搬椅子 | 6 | 8 | -- |
| 共搬椅子 | 6x | 8（65-x） | 400 |
可列出方程：6x+8（65-x）=400
解得：x=60．
分析 设A组同学有x人参加搬椅子，则其它组同学有（65-x）人参加搬椅子，搬椅子的总数=人数×每人搬的数量结合总共搬了400把椅子，即可得出关于x的一元一次方程，解之即可得出结论．
解答 解：设A组同学有x人参加搬椅子，则其它组同学有（65-x）人参加搬椅子，
根据题意得：6x+8（65-x）=400，
解得：x=60．
故答案为：65-x；6x；8（65-x）；6x+8（65-x）=400；60．
点评 本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．
练习册系列答案
相关题目
8．
如图，在四边形ABCD中，DC∥AB，CB⊥AB，AB=AD=2CD，点E，F分别为AB，AD的中点，则三角形AEF与多边形BCDFE的面积之比为（ ）
如图，在四边形ABCD中，DC∥AB，CB⊥AB，AB=AD=2CD，点E，F分别为AB，AD的中点，则三角形AEF与多边形BCDFE的面积之比为（ ）| A． | 1：7 | B． | 1：6 | C． | 1：5 | D． | 1：4 |
11．
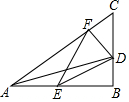如图，△ABC中，∠B=90°，∠C=60°，AD平分∠BAC交BC于D，过D作DF⊥AC于F，E在AB上，且DE=AE，连结EF．若AB=4+2$\sqrt{3}$，则EF的长为（ ）
如图，△ABC中，∠B=90°，∠C=60°，AD平分∠BAC交BC于D，过D作DF⊥AC于F，E在AB上，且DE=AE，连结EF．若AB=4+2$\sqrt{3}$，则EF的长为（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{5}$ | D． | 2$\sqrt{5}$ |
8．下列计算正确的是（ ）
| A． | （3xy2）2=6xy4 | B． | a+2a2=3a3 | C． | （-x）7÷（-x）2=-x5 | D． | 3x2+4x2=7x4 |
6．
某报社为了解我市市民对大范围雾霾天气的成因、影响以及应对措施的看法，做了一次抽样调查，其中有一个问题是：“您觉得雾霾天气对您哪方面的影响最大？”五个选项分别是：A．身体健康；B．出行；C．情绪不爽；D．工作学习；E．基本无影响，根据调查统计结果，绘制了如下三幅尚不完整的三种统计图、表：
（1）本次参与调查的市民共有200人，m=65%，n=5%；
（2）请将条形统计图补充完整；
（3）扇形统计图中A部分的圆心角的度数是234°；
（4）根据调查结果．学校准备开展关于雾霾知识竞赛，某班要从小明和小刚中选一人参加，现设计了如下游戏来确定：在一个不透明的袋中装有2个红球和3个白球，它们除了颜色外都相同，小明先从袋中随机摸出一个球，小刚再从剩下的四个球中随机摸出一个球，若摸出的两个球颜色相同，则小明去；否则小刚去．现在，小明同学摸出了一个白球，则小明参加竞赛的概率为多少？
某报社为了解我市市民对大范围雾霾天气的成因、影响以及应对措施的看法，做了一次抽样调查，其中有一个问题是：“您觉得雾霾天气对您哪方面的影响最大？”五个选项分别是：A．身体健康；B．出行；C．情绪不爽；D．工作学习；E．基本无影响，根据调查统计结果，绘制了如下三幅尚不完整的三种统计图、表：| 雾霾天气对您哪方面的影响最大 | 百分比 |
| A． 身体健康 | m |
| B． 出行 | 15% |
| C．情绪不爽 | 10% |
| D． 工作学习 | n |
| E． 基本无影响 | 5% |
（2）请将条形统计图补充完整；
（3）扇形统计图中A部分的圆心角的度数是234°；
（4）根据调查结果．学校准备开展关于雾霾知识竞赛，某班要从小明和小刚中选一人参加，现设计了如下游戏来确定：在一个不透明的袋中装有2个红球和3个白球，它们除了颜色外都相同，小明先从袋中随机摸出一个球，小刚再从剩下的四个球中随机摸出一个球，若摸出的两个球颜色相同，则小明去；否则小刚去．现在，小明同学摸出了一个白球，则小明参加竞赛的概率为多少？