题目内容
已知?ABCD中，AB=4，AD=2，E是AB边上的一动点，设AE=x，DE延长线交CB的延长线于F，设CF=y，求y与x之间的函数关系．
解：∵四边形ABCD为平行四边形，
∴∠A=∠C，∠ADE=∠F，
∴△ADE∽△CFD
∴
=
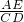，即
=
，
∴y=
．
分析：由平行四边形的性质，利用“角角”证明△ADE∽△CFD，根据相似三角形对应边的比相等，得出y与x之间的函数关系．
点评：本题考查了平行四边形的性质及相似三角形的判断、性质的运用．
∴∠A=∠C，∠ADE=∠F，
∴△ADE∽△CFD
∴
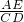=，即=，∴y=
．分析：由平行四边形的性质，利用“角角”证明△ADE∽△CFD，根据相似三角形对应边的比相等，得出y与x之间的函数关系．
点评：本题考查了平行四边形的性质及相似三角形的判断、性质的运用．
练习册系列答案
相关题目
19、已知?ABCD中，∠A的平分线AE交CD于E且DE=4，EC=5，求?ABCD的周长．
（2011•裕华区一模）如图，已知□ABCD中，E、F分别是边AD、BC的中点，AC分别交BE、DF于G、H，请观察下列结论：①BE=DF；②AG=GH=HC；③EG：BG=1：2；④S△AHD=2S△AGE；⑤AG；AC=1：3．其中结论正确的有（填序号）
如图，已知?ABCD中，AE平分∠BAD，CF平分∠BCD，分别交BC、AD于E、F．
如图，已知?ABCD中，AB=4，BC=6，BC边上的高AE=2，求DC边上的高AF的长．