题目内容
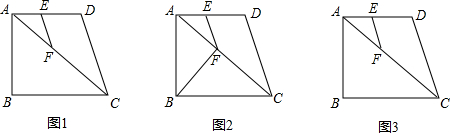
 (2011•裕华区一模)如图,已知□ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,请观察下列结论:①BE=DF;②AG=GH=HC;③EG:BG=1:2;④S△AHD=2S△AGE;⑤AG;AC=1:3.其中结论正确的有(填序号)
(2011•裕华区一模)如图,已知□ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,请观察下列结论:①BE=DF;②AG=GH=HC;③EG:BG=1:2;④S△AHD=2S△AGE;⑤AG;AC=1:3.其中结论正确的有(填序号)①②③⑤
①②③⑤
.分析:根据平行四边形的性质求出AB∥CD,AD∥BC,AD=BC,AB=CD,证平行四边形DEBF,推出BE∥DF,证△AGB≌△CHD,即可推出①②⑤,根据相似三角形性质即可推出④,根据DH=BG,即可推出③.
解答:解:∵平行四边形ABCD,
∴AD∥BC,AD=BC,
∵E、F分别是边AD、BC的中点,
∴DE=
AD,BF=
BC,
∴DE=CF,DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF,∴①正确;
∴BE∥DF,
∵E、F分别是边AD、BC的中点,
∴AG=GH=CH,∴②正确;⑤正确;
∴EG=
DH,
∵平行四边形ABCD,
∴AB∥CD,AB=CD,
∴∠BAC=∠DCA,
∵BE∥DF,
∴∠DHC=∠EGH,
∵∠EGH=∠AGB,
∴∠AGB=∠DHC,
∴△AGB≌△CHD(AAS),
∴DH=BG,
∴EG=
BG,∴③正确;
∵BE∥DF,
∴△AEG∽△ADH,
∴S△ADH=4S△ADH,∴④错误;
正确的有①②③⑤.
故答案为:①②③⑤.
∴AD∥BC,AD=BC,
∵E、F分别是边AD、BC的中点,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=CF,DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF,∴①正确;
∴BE∥DF,
∵E、F分别是边AD、BC的中点,
∴AG=GH=CH,∴②正确;⑤正确;
∴EG=
| 1 |
| 2 |
∵平行四边形ABCD,
∴AB∥CD,AB=CD,
∴∠BAC=∠DCA,
∵BE∥DF,
∴∠DHC=∠EGH,
∵∠EGH=∠AGB,
∴∠AGB=∠DHC,
∴△AGB≌△CHD(AAS),
∴DH=BG,
∴EG=
| 1 |
| 2 |
∵BE∥DF,
∴△AEG∽△ADH,
∴S△ADH=4S△ADH,∴④错误;
正确的有①②③⑤.
故答案为:①②③⑤.
点评:本题考查了平行四边形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定等知识点的运用,关键是考查学生对这些性质的综合运用能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
(2011•裕华区二模)一鞋店试销一种新款女鞋,试销期间卖出情况如下表:
对于这个鞋店的经理来说最关心哪种型号鞋畅销,则下列统计量对鞋店经理来说最有意义的是( )
A.平均数
B.中位数
C.方差
D.众数
| 型号 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 数量(双) | 3 | 5 | 10 | 15 | 8 | 3 | 2 |
A.平均数
B.中位数
C.方差
D.众数