Question

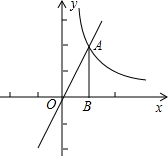如图，直线y=2x与双曲线y=在第一象限的交点为A，过点A作AB⊥x轴于B，将△ABO绕点O旋转90°，得到△A′B′O，则点A′的坐标为

1. A.
   （1.0）
2. B.
   （1.0）或（-1.0）
3. C.
   （2.0）或（0，-2）
4. D.
   （-2.1）或（2，-1）

Answer 1

D
分析：联立直线与反比例解析式，求出交点A的坐标，将△ABO绕点O旋转90°，得到△A′B′O，利用图形及A的坐标即可得到点A′的坐标．
解答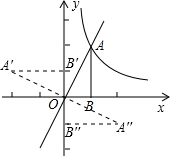：解：联立直线与反比例解析式得：，
消去y得到：x²=1，
解得：x=1或-1，
∴y=2或-2，
∴A（1，2），即AB=2，OB=1，
根据题意画出相应的图形，如图所示，
可得A′B′=A′′B′′=AB=2，OB′=OB′′=OB=1，
根据图形得：点A′的坐标为（-2，1）或（2，-1）．
故选D．
点评：此题考查了反比例函数与一次函数的交点问题，涉及的知识有：坐标与图形变化-旋转，作出相应的图形是解本题的关键．