题目内容
 (2012•甘孜州)如图,直线y=2x与y=
(2012•甘孜州)如图,直线y=2x与y=| k |
| x |
(1)求直线BC的解析式;
(2)若
| AO |
| BC |
分析:(1)根据直线平移可得到直线BC的解析式为y=2x+b,C点坐标为(3,0),然后把C点坐标代入求出b即可;
(2)作AD⊥x轴于D,BE⊥x轴于E,易得Rt△AOD∽Rt△BCE,则OD:CE=AD:BE=AO:BC=2,设OD=t,则CE=
t,利用A点在直线y=2x上得到AD=2t,则BE=t,于是得到A点坐标为(t,2t),B点坐标为(3+
t,t),然后根据反比例函数图象上点的坐标特征得到k=t•2t=(3+
t)•t,再求出t后计算k的值.
(2)作AD⊥x轴于D,BE⊥x轴于E,易得Rt△AOD∽Rt△BCE,则OD:CE=AD:BE=AO:BC=2,设OD=t,则CE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)∵直线y=2x向右平移3个单位,与x轴交于点C,
解:(1)∵直线y=2x向右平移3个单位,与x轴交于点C,
∴C点坐标为(3,0),直线BC的解析式可设为y=2x+b,
把C(3,0)代入y=2x+b得6+b=0,解得b=-6,
所以直线BC的解析式为y=2x-6;
(2)作AD⊥x轴于D,BE⊥x轴于E,如图,
∵OA∥BC,
∴∠AOC=∠BCE,
∴Rt△AOD∽Rt△BCE,
∴OD:CE=AD:BE=AO:BC=2,
设OD=t,则CE=
t,
把x=t代入y=2x得y=2t,
∴AD=2t,
∴BE=t,
∴A点坐标为(t,2t),B点坐标为(3+
t,t),
∵点A与点B都在反比例函数y=
上,
∴k=t•2t=(3+
t)•t,
解得t1=2,t2=0(舍去),
∴k=2×4=8.
 解:(1)∵直线y=2x向右平移3个单位,与x轴交于点C,
解:(1)∵直线y=2x向右平移3个单位,与x轴交于点C,∴C点坐标为(3,0),直线BC的解析式可设为y=2x+b,
把C(3,0)代入y=2x+b得6+b=0,解得b=-6,
所以直线BC的解析式为y=2x-6;
(2)作AD⊥x轴于D,BE⊥x轴于E,如图,
∵OA∥BC,
∴∠AOC=∠BCE,
∴Rt△AOD∽Rt△BCE,
∴OD:CE=AD:BE=AO:BC=2,
设OD=t,则CE=
| 1 |
| 2 |
把x=t代入y=2x得y=2t,
∴AD=2t,
∴BE=t,
∴A点坐标为(t,2t),B点坐标为(3+
| 1 |
| 2 |
∵点A与点B都在反比例函数y=
| k |
| x |
∴k=t•2t=(3+
| 1 |
| 2 |
解得t1=2,t2=0(舍去),
∴k=2×4=8.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标同时满足两个函数的解析式.也考查了一次函数图象与几何变换和三角形相似的判定与性质.

练习册系列答案
相关题目
 (2012•甘孜州)如图放置的圆锥,它的主视图、俯视图、左视图分别为( )
(2012•甘孜州)如图放置的圆锥,它的主视图、俯视图、左视图分别为( )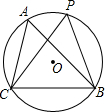 (2012•甘孜州)如图.⊙O是△ABC的外接圆,∠CAB=65°,P是⊙O上的一点,则∠CPB等于( )
(2012•甘孜州)如图.⊙O是△ABC的外接圆,∠CAB=65°,P是⊙O上的一点,则∠CPB等于( ) (2012•甘孜州)如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )
(2012•甘孜州)如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )