题目内容
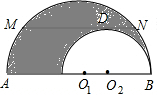 如图,已知大半圆⊙O1与小半圆⊙O2相内切于点B,大半圆的弦MN切小半圆于点D,若MN∥AB,当MN=5时,则此图中的阴影部分的面积是
如图,已知大半圆⊙O1与小半圆⊙O2相内切于点B,大半圆的弦MN切小半圆于点D,若MN∥AB,当MN=5时,则此图中的阴影部分的面积是考点:切线的性质,勾股定理,垂径定理
专题:计算题
分析:作O1H⊥MN于H,连结O2D,O1N,如图,根据切线的性质得O2D⊥MN,而MN∥AB,可判断四边形O1O2DH为矩形,则O2D=O1H,再根据垂径定理,由O1H⊥MN得到MH=MH=
MN=
,在Rt△O1NH中,利用勾股定理得到O1N2-O1H2=NH2=
,则O1N2-O2D2=
,然后根据圆的面积公式得到图中的阴影部分的面积=
(πO1N2-πO2D2),再利用整体代入的方法计算即可.
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 4 |
| 25 |
| 4 |
| 1 |
| 2 |
解答: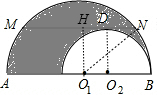 解:作O1H⊥MN于H,连结O2D,O1N,如图,
解:作O1H⊥MN于H,连结O2D,O1N,如图,
∵大半圆⊙O1与小半圆⊙O2相内切于点B,
∴点O2在O1B上,
∵大半圆的弦MN切小半圆于点D,
∴O2D⊥MN,
而MN∥AB,
∴四边形O1O2DH为矩形,
∴O2D=O1H,
∵O1H⊥MN,
∴MH=MH=
MN=
,
在Rt△O1NH中,O1N2-O1H2=NH2=
∴O1N2-O2D2=
∵图中的阴影部分的面积=
(S大半圆-S小半圆)
=
(πO1N2-πO2D2)
=
π•(O1N2-O2D2)
=
π•
=
π.
故答案为
π.
 解:作O1H⊥MN于H,连结O2D,O1N,如图,
解:作O1H⊥MN于H,连结O2D,O1N,如图,∵大半圆⊙O1与小半圆⊙O2相内切于点B,
∴点O2在O1B上,
∵大半圆的弦MN切小半圆于点D,
∴O2D⊥MN,
而MN∥AB,
∴四边形O1O2DH为矩形,
∴O2D=O1H,
∵O1H⊥MN,
∴MH=MH=
| 1 |
| 2 |
| 5 |
| 2 |
在Rt△O1NH中,O1N2-O1H2=NH2=
| 25 |
| 4 |
∴O1N2-O2D2=
| 25 |
| 4 |
∵图中的阴影部分的面积=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 25 |
| 4 |
=
| 25 |
| 8 |
故答案为
| 25 |
| 8 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了勾股定理、垂径定理.

练习册系列答案
相关题目
4a-a的计算结果是( )
| A、3 | B、3a | C、4 | D、4a |
 如图,在一个直角边长分别为10米、30米的三角形花园旁边有一个正方形的运动场,这个运动场的面积是
如图,在一个直角边长分别为10米、30米的三角形花园旁边有一个正方形的运动场,这个运动场的面积是 如图,如果AB∥CD,BC∥ED,那么∠B+∠D等于多少度?
如图,如果AB∥CD,BC∥ED,那么∠B+∠D等于多少度?