题目内容
18.若n是正整数,47+4n+23996是一个整数的平方,求n的值.分析 本题分两种情况讨论n的取值,首先把47+4n+23996化简为完全平方式的形式,然后根据化简后的式子得出n.
解答 解:①47+4n+23996
=(27)2+2•27•22n-8+(21998)2,
∵47+4n+23996是一个完全平方数.
∴22n-8=21998,
即2n-8=1998,
∴当n=1003时,47+4n+23996是完全平方数;
②47+4n+23996
=47+23996+4n
=(27)2+2•27•23988+(2n)2,
∵47+4n+23996是一个完全平方数.
∴23988=2n,
∴n=3988.
综上得n=1003或n=3988.
点评 此题考查了完全平方数的知识.注意把47+4n+23996化简为完全平方式的形式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列各数中,是有理数是( )
| A. | $\frac{22}{7}$ | B. | π | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
7. 某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
 某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )| A. | a=20 | |
| B. | b=4 | |
| C. | 若工人甲一天获得薪金180元,则他共生产50件 | |
| D. | 若工人乙一天生产m(件),则他获得薪金4m元 |
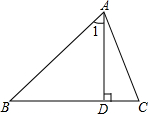 如图,AD是△ABC的高,∠1=∠B,∠C=65°,则∠BAC=70°.
如图,AD是△ABC的高,∠1=∠B,∠C=65°,则∠BAC=70°.