Question

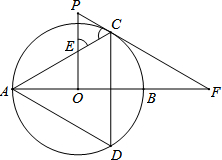如图，以AB为直径的⊙O是△ADC的外接圆，过点O作PO⊥AB，交AC于点E，PC的延长线交AB的延长线于点F，∠PEC=∠PCE．若△ADC是边长为1的等边三角形，则PC的长=________．

Answer 1

分析：根据圆内接正三角形的性质得出AB⊥CD，∠NCO=30°，进而得出NO=CO=AO，再利用PO∥CD，得出=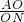的值，再得出△PEC是等边三角形，进而得出答案．
解答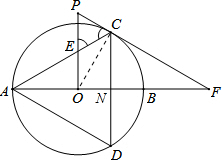：解：∵△ADC是边长为1的等边三角形，AB为⊙O的直径，
∴AB⊥CD，连接CO，
∴CO=AO，∠NCO=30°，
∴NO=CO=AO，
∵PO⊥AB，AB⊥CD，
∴PO∥CD，
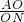∴==2，
∵∠ACD=60°，PO∥CD，
∴∠CEP=60°，
∵PE=PC，
∴△PEC是等边三角形，
∴EC=PC=PE=AC=．
故答案为：．
点评：此题主要考查了圆内接正三角形的性质以及平行线分线段成比例定理和等边三角形的判定等知识，根据已知得出=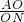的值是解题关键．