题目内容
8.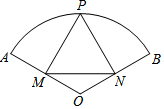 如图扇形OAPB是半径为2的⊙O的一部分,点P是弧AB上一点,PM⊥AO,PN⊥BO,垂足分别为M、N,且∠AOB=120°.
如图扇形OAPB是半径为2的⊙O的一部分,点P是弧AB上一点,PM⊥AO,PN⊥BO,垂足分别为M、N,且∠AOB=120°.(1)当点P为$\widehat{AB}$的中点时,求线段MN的长度.
(2)当点P为$\widehat{AB}$上一动点时,不与点A、B重合,判断线段MN的长度是否为定值.
分析 (1)如图1,延长PM,PN分别交⊙O于E,F,连接PO,根据四边形的内角和得到∠MPN=60°,根据全等三角形的性质得到PM=PN,根据垂径定理得到PE=2PM,PF=2PN,推出△PEF是等边三角形,根据三角形的中位线的性质即可得到结论;
(2)延长PM,PN交⊙O于Q,S,根据垂径定理得到PM=QM,PN=NS,根据等腰三角形的性质得到∠POA=∠QOA,∠PON=∠SON,根据周角的定义得到∠QOS=120°,过O作OK⊥QS于K,解直角三角形得到结论.
解答  解:(1)如图1,延长PM,PN分别交⊙O于E,F,连接PO,
解:(1)如图1,延长PM,PN分别交⊙O于E,F,连接PO,
∵PM⊥AO,PN⊥BO,
∴∠PMO=∠PNO=90°,
∵∠AOB=120°,
∴∠MPN=60°,
∵点P为$\widehat{AB}$的中点,
∴∠POM=∠PON,
在△POM与△PON中,$\left\{\begin{array}{l}{∠PMO=∠PNO}\\{∠POM=∠PON}\\{OP=OP}\end{array}\right.$,
∴△PMO≌△PNO,
∴PM=PN,
∵PM⊥AO,PN⊥BO,
∴PE=2PM,PF=2PN,
∴PE=PF,
∴△PEF是等边三角形,
∴PE=EF,
∵OP=2,
∴PM=PN=$\sqrt{3}$,
∴EF=2$\sqrt{3}$,
∴MN=$\frac{1}{2}$EF=$\sqrt{3}$;
(2)延长PM,PN交⊙O于Q,S,
∵PM⊥AO,PN⊥BO,
∴PM=QM,PN=NS,
∵OP=OQ=OS,
∴∠POA=∠QOA,∠PON=∠SON,
∴∠QOS=120°,
过O作OK⊥QS于K,
∴∠QOK=60°,QK=SK,∴QK=$\frac{\sqrt{3}}{2}$OQ=$\sqrt{3}$,
∴QS=2$\sqrt{3}$,
∴MN=$\frac{1}{2}$QS=$\sqrt{3}$(定值),
∴MN的长度是定值.
点评 此题考查了垂径定理,勾股定理,以及三角形的中位线定理,熟练掌握定理是解本题的关键.

| A. | 2和3 | B. | 4和5 | C. | 5和7 | D. | 35和36 |
| A. |  | B. |  | C. |  | D. |  |
| A. | (-a+b)(a-b) | B. | (a-b)(a-2b) | C. | (x+1)(x-1) | D. | (-m-n)(m+n) |
| A. | 14×104 | B. | 1.4×102 | C. | 14×105 | D. | 1.4×106 |
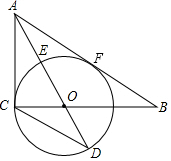 如图,Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
如图,Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O. 如图,将一副三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,若∠AOC=70°,则∠BOD的度数为70°.
如图,将一副三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,若∠AOC=70°,则∠BOD的度数为70°.