题目内容
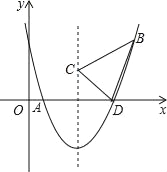
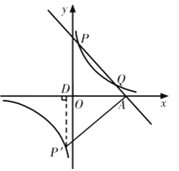
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.

【答案】(1)y=﹣2x+9;(2)(-![]() ,﹣8);(3)
,﹣8);(3)![]()
【解析】试题分析:(1)根据P(![]() ,8),可得反比例函数解析式,根据P(
,8),可得反比例函数解析式,根据P(![]() ,8),Q(4,1)两点可得一次函数解析式;
,8),Q(4,1)两点可得一次函数解析式;
(2)根据中心对称的性质,可得点P关于原点的对称点P'的坐标;
(3)过点P′作P′D⊥x轴,垂足为D,构造直角三角形,依据P'D以及AP'的长,即可得到∠P'AO的正弦值.
试题解析:(1)∵点P在反比例函数的图象上,∴把点P(![]() ,8)代入
,8)代入![]() 可得:k2=4,∴反比例函数的表达式为
可得:k2=4,∴反比例函数的表达式为![]() ,∴Q (4,1).
,∴Q (4,1).
把P(![]() ,8),Q (4,1)分别代入
,8),Q (4,1)分别代入![]() 中,得:
中,得: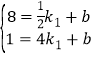 ,解得:
,解得:![]() ,∴一次函数的表达式为y=﹣2x+9;
,∴一次函数的表达式为y=﹣2x+9;
(2)点P关于原点的对称点P'的坐标为(![]() ,﹣8);
,﹣8);
(3)过点P′作P′D⊥x轴,垂足为D.
∵P′(![]() ,﹣8),∴OD=
,﹣8),∴OD=![]() ,P′D=8,∵点A在y=﹣2x+9的图象上,∴点A(
,P′D=8,∵点A在y=﹣2x+9的图象上,∴点A(![]() ,0),即OA=
,0),即OA=![]() ,∴DA=5,∴P′A=
,∴DA=5,∴P′A=![]() =
=![]() ,∴sin∠P′AD=
,∴sin∠P′AD=![]() =
=![]() ,∴sin∠P′AO=
,∴sin∠P′AO=![]() .
.

练习册系列答案
相关题目