题目内容
12.计算与化简:(1)($\frac{x}{x+y}$+$\frac{2y}{x+y}$)•$\frac{xy}{x+2y}$÷($\frac{1}{x}$+$\frac{1}{y}$);
(2)($\frac{1}{a}$+$\frac{1}{b}$)2÷($\frac{1}{{a}^{2}}$-$\frac{1}{{b}^{2}}$)
分析 (1)首先对括号内的分式通分相减,把除法转化为乘法,然后进行乘法运算即可;
(2)首先对括号内的分式通分相减,把除法转化为乘法,然后进行乘法运算即可.
解答 解:(1)原式=$\frac{x+2y}{x+y}$•$\frac{xy}{x+2y}$÷$\frac{x+y}{xy}$
=$\frac{x+2y}{x+y}$•$\frac{xy}{x+2y}$•$\frac{xy}{x+y}$
=$\frac{{x}^{2}{y}^{2}}{(x+y)^{2}}$;
(2)原式=($\frac{a+b}{ab}$)2÷$\frac{{b}^{2}-{a}^{2}}{{a}^{2}{b}^{2}}$
=$\frac{(a+b)^{2}}{{a}^{2}{b}^{2}}$•$\frac{{a}^{2}{b}^{2}}{(a+b)(b-a)}$
=$\frac{a+b}{b-a}$.
点评 本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
相关题目
2.某年11月份有一个星期,从星期一到星期五连续五天的日历数字之和为55,则这个月的12号是( )
| A. | 星期一 | B. | 星期二 | C. | 星期三 | D. | 星期四 |
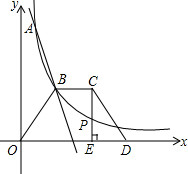 如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)(x>0)的图象交于A(1,6),B(a,3)两点,
如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)(x>0)的图象交于A(1,6),B(a,3)两点,